题目内容
(本题满分14分)
已知点M在椭圆+=1(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点F.
(1)若圆M与y轴相切,求椭圆的离心率;
(2)若圆M与y轴相交于A,B两点,且△ABM是边长为2的正三角形,求椭圆的方程.
(1)解:由题意可知,点M的坐标为(c,c),∴![]() , …………2分
, …………2分
即![]() ,即
,即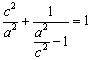 ,即
,即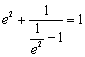 ,即
,即![]() ,
,
即![]() ,即e4-3e2+1=0,∴
,即e4-3e2+1=0,∴![]() ,……5分
,……5分
∴e=![]() ,又e∈(0,1),∴e=
,又e∈(0,1),∴e=![]() 。 ………………………………7分
。 ………………………………7分
(2)解:把x=c代入椭圆方程+=1,得yM=±。
因为△ABM是边长为2的正三角形,
所以圆M的半径r=2.M到y轴的距离d=.
∴r=,d=c,
即c=,=2. …………………………………………………………………11分
又因为a2-b2=c2.
所以a2-b2=3.
代入得a2-2a-3=0,a=3,a=-1(舍去).
b2=2a=6.
所以所求的椭圆方程为+=1.…………………………………………………14分

练习册系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).