题目内容
【题目】我国古代数学典籍《九章算术》第七章“盈不足”中有一道两鼠穿墙问题：“今有垣厚五尺，两鼠对穿，大鼠日一尺，小鼠日一尺，大鼠日自倍，小鼠日自半，问何日相逢，各穿几何”，翻译过来就是：有五尺厚的墙，两只老鼠从墙的两边相对分别打洞穿墙，大、小鼠第一天都进一尺，以后每天，大鼠加倍，小鼠减半，则几天后两鼠相遇，这个问题体现了古代对数列问题的研究，现将墙的厚度改为1200尺，则需要几天时间才能打穿（结果取整数）（ ）
A.12B.11C.10D.9
【答案】B
【解析】
大鼠和小鼠每天穿墙尺寸都构成一个等比数列，只是公比不同，然后由等比数列前
项和公式计算可得．
大鼠和小鼠每天穿墙尺寸分别构成数列
，它们都是等比数列，
，数列
的公比为
，数列
的公比为
，设需要天能打穿墙，
则
，
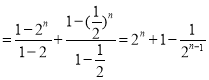时，
，
时，
，
因此需要11天才能打穿．
故选：B.
字词句篇与同步作文达标系列答案
【题目】A药店计划从甲，乙两家药厂选择一家购买100件某种中药材，为此A药店从这两家药厂提供的100件该种中药材中随机各抽取10件，以抽取的10件中药材的质量（单位:克》作为样本.样本数据的茎叶图如图所示.己知A药店根据中药材的质量（单位:克）的往定性选择药厂
（1）根据样本数据，A药店应选择哪家药厂购买中药材?
（2）若将抽取的样本分布近似看作总体分布，药店与所选药厂商定中药材的购买价格如下表:
每件中药材的质量（单位:克） | 购买价格（单位:元/件） |
|
|
|
|
|
|
（i）估计
药店所购买的
件中药材的总质量;
（ii）若药店所购买的件中药材的总费用不超过
元.求
的最大值.
【题目】王久良导演的纪录片《垃圾围城》真实地反映了城市垃圾污染问题，目前中国668个城市中有超过
的城市处于垃圾的包围之中，且城市垃圾中的快递行业产生的包装垃圾正在逐年攀升，有关数据显示，某城市从2016年到2019年产生的包装垃圾量如下表：
年份x | 2016 | 2017 | 2018 | 2019 |
包装垃圾y（万吨） | 4 | 6 | 9 | 13.5 |
（1）有下列函数模型：①
；②
；③
.
试从以上函数模型中，选择模型________（填模型序号），近似反映该城市近几年包装垃圾生产量y（万吨）与年份x的函数关系，并直接写出所选函数模型解析式；
（2）若不加以控制，任由包装垃圾如此增长下去，从哪年开始，该城市的包装垃圾将超过40万吨？（参考数据：
）