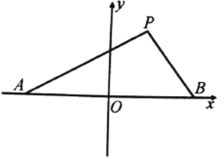
题目内容
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 与
与![]() 的交点为
的交点为![]() .
.
(1)判断点![]() 与曲线
与曲线![]() 的位置关系;
的位置关系;
(2)点![]() 为曲线
为曲线![]() 上的任意一点,求
上的任意一点,求![]() 的最大值.
的最大值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)先联立两直线的极坐标方程,求出交点的极坐标,再利用互化公式得到交点的直角坐标,消参得到曲线的普通方程,代点判定点和曲线的位置关系;(2)利用两点间的距离公式和二次函数的最值进行求解.
试题解析:(1)法一:由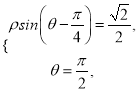 得
得![]() ,
,
所以![]() 与
与![]() 的交点
的交点![]() 的极坐标为
的极坐标为![]() ,即点
,即点![]() 的直角坐标为
的直角坐标为![]() .
.
又曲线C的普通方程为![]() ,
,
且![]() ,所以点M在曲线
,所以点M在曲线![]() 上.
上.
法二:直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,直线
,直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
由![]() 得
得![]() 所以
所以![]() 与
与![]() 的交点
的交点![]() 的直角坐标为
的直角坐标为![]() .
.
又曲线C的普通方程为![]() ,且
,且![]() ,所以点M在曲线
,所以点M在曲线![]() 上.
上.
(2)法一:设点P的直角坐标为![]() ,
,
![]() ,
,
当![]() 时,
时, ![]() ,
,
所以![]() 的最大值为
的最大值为![]() .
.
法二:设点P![]() ,其中
,其中![]() ,
,
则![]() ,
,
所以当![]() 时,
时, ![]() ,
,
所以![]() 的最大值为
的最大值为![]() .
.

【题目】为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了300名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合计 | |
男大学生 | 180 | ||
女大学生 | 45 | ||
合计 | 200 |
(Ⅰ)根据题意完成表格;
(Ⅱ)是否有![]() 的把握认为愿意做志愿者工作与性别有关?
的把握认为愿意做志愿者工作与性别有关?
附:![]() ,
,![]()
| 0.5 | 0.40 | 0.25 | 0.15 | 0.10 |
| 0.455 | 0.708 | 1.323 | .072 | 2.706 |
【题目】某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
Ⅰ.请完成上面的列联表;
Ⅱ.根据列联表的数据,是否有![]() 的把握认为“成绩与班级有关系”.
的把握认为“成绩与班级有关系”.
参考公式与临界值表:![]() .
.