题目内容
已知数列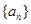 的前n项和
的前n项和 满足
满足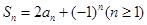
(1)写出数列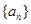 的前3项
的前3项 、
、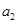 、
、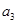 ;
;
(2)求数列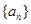 的通项公式;
的通项公式;
(3)证明对于任意的整数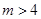 有
有
(1)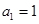 、
、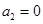 、
、 ;(2)
;(2)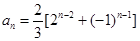 ;(3)见解析.
;(3)见解析.
解析试题分析:(1)是考查已知递推公式求前几项,属于基础题,需注意的是S1=a1,需要先求出a1才能求出a2,这是递推公式的特点;(2)解答需要利用公式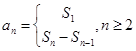 进行代换,要注意n=1和n≥2的讨论,在得到
进行代换,要注意n=1和n≥2的讨论,在得到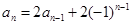 ,可以利用叠加法求解;(3)解答需要在代换后,适当的变形,利用不等式放缩法进行放缩.
,可以利用叠加法求解;(3)解答需要在代换后,适当的变形,利用不等式放缩法进行放缩.
试题解析:(1)由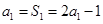 ,得
,得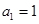 ,由
,由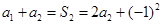 ,得
,得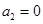 ,由
,由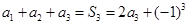 ,得
,得 ;(2)当
;(2)当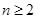 时,
时,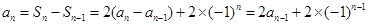 ,
,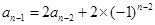 ,……,
,……,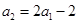
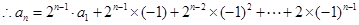
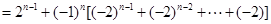
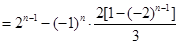
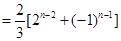 经验证:
经验证: 也满足上式,所以
也满足上式,所以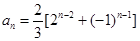 ,
,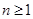 ;(3)证明:由通项知
;(3)证明:由通项知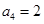 当
当 ,且n为奇数时
,且n为奇数时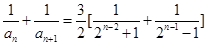
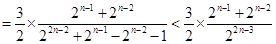
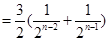
当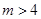 且m为偶数时
且m为偶数时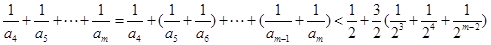
 ,当
,当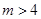 且m为奇数时
且m为奇数时 ∴对任意
∴对任意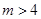 有
有
考点:1、递推数列;2、放缩法.

练习册系列答案
相关题目
 的首项
的首项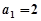 ,且对任意的
,且对任意的 都有
都有 ,则
,则 。
。 的前三项为
的前三项为 ,
, ,
, ,则
,则
 (n∈N*).
(n∈N*). ,计算a2,a3,a4的值,并求出数列{an}的通项公式.
,计算a2,a3,a4的值,并求出数列{an}的通项公式. 的前n项和为
的前n项和为 ,且
,且
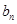 满足
满足 ,求数列
,求数列 的前n项和为
的前n项和为 ;
; 是数列
是数列 的前n项和,求证:
的前n项和,求证: 。
。 的前
的前 项和为
项和为 ,满足
,满足 ,
, ,且
,且 .
. 、
、 、
、 的值;
的值; 的通项公式.
的通项公式. 满足
满足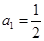 ,
, .
. 的值,由此猜测
的值,由此猜测 .
.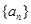 的前
的前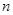 项和为
项和为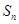 ,
,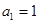 ,且
,且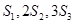 成等差数列.
成等差数列. ,求数列
,求数列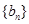 的前
的前 .
.