题目内容
在直角坐标系中,△ABC的三个顶点坐标分别为A(0,2),B(-1,0),C(1,0),动点P(x,y)是△ABC内的点(包括边界).若目标函数z=ax+by的最大值为2,且此时的最优解所确定的点P(x,y)是线段AC上的所有点,则目标函数z=ax+by的最小值为________.
-2
分析:先根据三顶点A(0,2),B(-1,0),C(1,0),画出可行域,设z=ax+by,再利用z的几何意义求最值,只需求出直线ax+by=z与可行域内的边BC平行时,z=ax+by取最大值时的最优解有无数个,从而得到a,b值,最后再求出目标函数z=ax+by的最小值即可.
解答: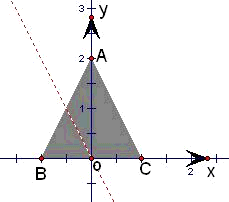 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,
设z=ax+by,
将最大值转化为y轴上的截距,
当直线ax+by=z与可行域内的边BC平行时,z=ax+by取最大值时的最优解有无数个,将- 等价为斜率,
等价为斜率,
数形结合,得 kAC=-2=- ,且a×1+b×0=2,
,且a×1+b×0=2,
∴a=2,b=1,z=2x+y
当直线z=2x+y过点B时,z取最小值,最小值为-2.
故答案为:-2.
点评:本题主要考查了简单线性规划,以及简单的转化思想和数形结合的思想,属中档题.
分析:先根据三顶点A(0,2),B(-1,0),C(1,0),画出可行域,设z=ax+by,再利用z的几何意义求最值,只需求出直线ax+by=z与可行域内的边BC平行时,z=ax+by取最大值时的最优解有无数个,从而得到a,b值,最后再求出目标函数z=ax+by的最小值即可.
解答:
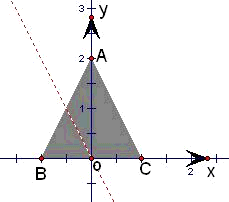 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,设z=ax+by,
将最大值转化为y轴上的截距,
当直线ax+by=z与可行域内的边BC平行时,z=ax+by取最大值时的最优解有无数个,将-
 等价为斜率,
等价为斜率,数形结合,得 kAC=-2=-
 ,且a×1+b×0=2,
,且a×1+b×0=2,∴a=2,b=1,z=2x+y
当直线z=2x+y过点B时,z取最小值,最小值为-2.
故答案为:-2.
点评:本题主要考查了简单线性规划,以及简单的转化思想和数形结合的思想,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
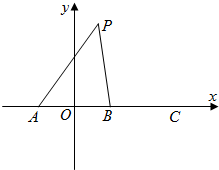 如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.
如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.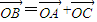 (O是坐标原点),其中t∈(0,+∞).
(O是坐标原点),其中t∈(0,+∞).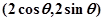
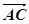 ^
^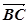 ,求
,求 的值;
的值;