题目内容
在直角坐标系中,A (1,t),C(-2t,2),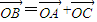 (O是坐标原点),其中t∈(0,+∞).
(O是坐标原点),其中t∈(0,+∞).(1)求四边形OABC在第一象限部分的面积S(t);
(2)确定函数S(t)的单调区间,并求S(t)的最小值.
【答案】分析:(1)先根据题意可判定四边形OABC的形状,然后讨论A在第一象限,B在第一象限,C在第二象限,然后利用S(t)=SOABC-S△OKC进行求解,A在第一象限,B在y轴上或在第二象限,C在第二象限,根据S(t)=S△OAM进行求解,最后利用分段函数表示即可;
(2)分别在每一段区间上利用导数符号判定函数的单调性,再根据单调性求出函数求S(t)的最小值.
解答: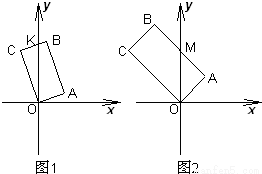 解:(1)∵
解:(1)∵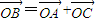 ,∴OABC为平行四边形,
,∴OABC为平行四边形,
又∵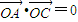 ,∴OA⊥OC,∴四边形OABC为矩形.
,∴OA⊥OC,∴四边形OABC为矩形.
∵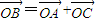 =(1-2t,2+t),
=(1-2t,2+t),
当1-2t>0,即0<t< 时,
时,
A在第一象限,B在第一象限,C在第二象限,(如图1)
此时BC的方程为:y-2=t(x+2t),
令x=0,得BC交y轴于K(0,2t2+2),
∴S(t)=SOABC-S△OKC=2(1-t+t2-t3).
当1-2t≤0,即t≥ 时,
时,
A在第一象限,B在y轴上或在第二象限,C在第二象限,(如图2)
此时AB的方程为:y-t=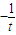 (x-1),令x=0,得AB交轴于M(0,t+
(x-1),令x=0,得AB交轴于M(0,t+ ),
),
∴S(t)=S△OAM=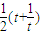 .
.
∴S(t)=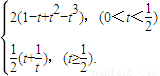
(2)当0<t< 时,S(t)=2(1-t+t2-t3),S′(t)=2(-1+2t-3t2)<0,
时,S(t)=2(1-t+t2-t3),S′(t)=2(-1+2t-3t2)<0,
∴S(t)在(0, )上是减函数.
)上是减函数.
当t≥ 时,S(t)=
时,S(t)=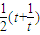 ,S′(t)=
,S′(t)=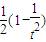 ,
,
∴S(t)在[ ,1]上是减函数,在(1,+∞)上是增函数.
,1]上是减函数,在(1,+∞)上是增函数.
∴当t=1时,S(t)有最小值为1.
点评:本题主要考查了函数的解析式,同时考查了函数的单调性和最值的求解,属于中档题.
(2)分别在每一段区间上利用导数符号判定函数的单调性,再根据单调性求出函数求S(t)的最小值.
解答:
 解:(1)∵
解:(1)∵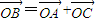 ,∴OABC为平行四边形,
,∴OABC为平行四边形,又∵
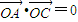 ,∴OA⊥OC,∴四边形OABC为矩形.
,∴OA⊥OC,∴四边形OABC为矩形.∵
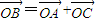 =(1-2t,2+t),
=(1-2t,2+t),当1-2t>0,即0<t<
 时,
时,A在第一象限,B在第一象限,C在第二象限,(如图1)
此时BC的方程为:y-2=t(x+2t),
令x=0,得BC交y轴于K(0,2t2+2),
∴S(t)=SOABC-S△OKC=2(1-t+t2-t3).
当1-2t≤0,即t≥
 时,
时,A在第一象限,B在y轴上或在第二象限,C在第二象限,(如图2)
此时AB的方程为:y-t=
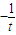 (x-1),令x=0,得AB交轴于M(0,t+
(x-1),令x=0,得AB交轴于M(0,t+ ),
),∴S(t)=S△OAM=
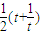 .
.∴S(t)=
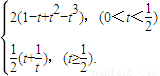
(2)当0<t<
 时,S(t)=2(1-t+t2-t3),S′(t)=2(-1+2t-3t2)<0,
时,S(t)=2(1-t+t2-t3),S′(t)=2(-1+2t-3t2)<0,∴S(t)在(0,
 )上是减函数.
)上是减函数.当t≥
 时,S(t)=
时,S(t)=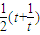 ,S′(t)=
,S′(t)=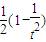 ,
,∴S(t)在[
 ,1]上是减函数,在(1,+∞)上是增函数.
,1]上是减函数,在(1,+∞)上是增函数.∴当t=1时,S(t)有最小值为1.
点评:本题主要考查了函数的解析式,同时考查了函数的单调性和最值的求解,属于中档题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
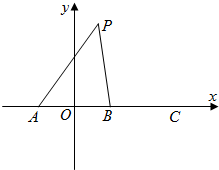 如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.
如图,在直角坐标系中,A,B,C三点在x轴上,原点O和点B分别是线段AB和AC的中点,已知AO=m(m为常数),平面上的点P满足PA+PB=6m.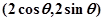
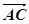 ^
^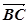 ,求
,求 的值;
的值;