Question

【题目】已知数列{an}是首项 ，公比 的等比数列．设 （n∈N*）． （Ⅰ）求证：数列{bn}为等差数列；
（Ⅱ）设cn=an+b2n ， 求数列{cn}的前n项和Tn ．

Answer 1

【答案】解：（Ⅰ）证明：∵数列{an}是首项 ，公比 的等比数列， ∴ ，则 = ．
∴bn+1﹣bn=[2（n+1）﹣1]﹣（2n﹣1）=2．
则数列{bn}是以2为公差的等差数列；
（Ⅱ）解：cn=an+b2n= ．
∴数列{cn}的前n项和Tn=c1+c2+…+cn=[ ]+4（1+2+…+n）﹣n
= = = ．
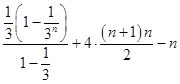【解析】（Ⅰ）由已知求出等比数列的通项公式，代入 可得数列{bn}的通项公式，由等差数列的定义证明数列{bn}为等差数列；（Ⅱ）把数列{an}、{bn}的通项公式代入cn=an+b2n ， 分组后再由等差数列与等比数列的前n项和求数列{cn}的前n项和Tn ．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系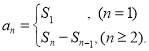；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．