题目内容
10．不等式|x-1|+2|x+1|＜3的解集为（-$\frac{4}{3}$，0）．分析 把要解的不等式等价转化为与之等价的三个不等式组，求出每个不等式组的解集，再取并集，即得所求．
解答 解：由不等式|x-1|+2|x+1|＜3，可得 $\left\{\begin{array}{l}{x＜-1}\\{-3x-1＜3}\end{array}\right.$①，或 $\left\{\begin{array}{l}{-1≤x＜1}\\{x+3＜3}\end{array}\right.$②，或 $\left\{\begin{array}{l}{x≥1}\\{3x+1＜3}\end{array}\right.$③．
解①求得-$\frac{4}{3}$＜x＜-1，解②求得-1≤x＜0，解③求得x∈∅．
综上可得，原不等式的解集为（-$\frac{4}{3}$，0），
故答案为：（-$\frac{4}{3}$，0）．
点评 本题主要考查绝对值不等式的解法，体现了转化、分类讨论的数学思想，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
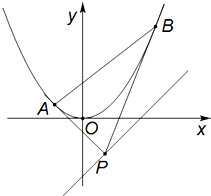已知直线l的方程是y=x-1和抛物线C：x2=y，自l上任意一点P作抛物线的两条切线，设切点分别为A，B，