题目内容
3.已知等差数列{an}中,公差d>0,且a2、a6是一元二次方程$\frac{1}{2}$x2-8x+14=0的根.(1)求数列{an}的通项公式an.
(2)求数列{an}的前10项和.
分析 (1)由韦达定理得a2=2,a2=14,由此利用等差数列通项公式能求出首项和公差,由此能求出通项公式.
(2)由等差数列的首项和公差,能求出数列{an}的前10项和.
解答 解:(1)由题意得:一元二次方程$\frac{1}{2}{x}^{2}-8x+14=0$的根为2,14,
∵公差d>0,∴a2=2,a2=14,…(1分)
即$\left\{\begin{array}{l}{{a}_{1}+d=2}\\{{a}_{1}+5d=14}\end{array}\right.$,…(2分)
解得a1=-1,d=3,…(3分)
∴通项公式an=-1+(n-1)×3=3n-4.…(5分)
(2)∵得a1=-1,d=3,
∴S10=$10×(-1)+\frac{10×9}{2}×3$=125.…(7分)
点评 本题考查等差数列的通项公式和前n项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
13.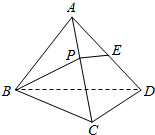 如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )
如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )
 如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )
如图所示,在棱长为2的正四面体A-BCD中,E是棱AD的中点,若P是棱AC上一动点,则BP+PE的最小值为( )| A. | 3 | B. | $\sqrt{7}$ | C. | 1+$\sqrt{3}$ | D. | $\sqrt{5}$ |
18.设f(x)是定义在R上的奇函数,且在[0,+∞)上单调递增,则f(-3),f(-4)的大小关系是( )
| A. | f (-3)>f (-4) | B. | f (-3)<f (-4) | C. | f (-3)=f (-4) | D. | 无法比较 |
8.在△ABC中,角A、B、C所对边分别为a、b、c,若asinB=2bsinAcosC,则角C的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
13.数列a,a,a,a…,(a∈R)必为( )
| A. | 等差数列 | B. | 等比数列 | ||
| C. | 既是等差数列,又是等比数列 | D. | 以上都不正确 |