题目内容
16．设函数f（x）=arcsin（cos（x）），则f（f（f（x）））的最小正周期为π．分析 现根据函数的周期性的定义求得f（x）的最小正周期是2π，再根据f（x）是偶函数，可得f[f（x）]的最小正周期是π，从而得到 f{f[f（x）]}的最小正周期．
解答 解：∵f（x+2π）=arcsin（cos（x+2π））=arcsin（cos（x））=f（x），∴f（x）的最小正周期是2π．
又f（x）是偶函数，f（x+π）=-f（x），∴f[f（x+π）]=f[-f（x）]=f[f（x）]，
∴f[f（x）]的最小正周期是π，∴f{f[f（x）]}的最小正周期是π，
故答案为：π．
点评 本题主要考查三角函数的周期性和奇偶性，属于基础题．
练习册系列答案
相关题目
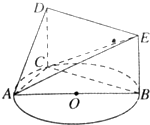如图所示，已知△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，DC⊥平面ABC，AB=2，tan∠EAB=$\frac{1}{2}$．