题目内容
12、已知f(x)=asin(πx+α)+bcos(πx+β),其中a、b、α、β都是非零常数,若f(2009)=-1,则f(2010)等于( )
分析:先根据诱导公式对f(2009)的解析式化简整理,把x=2010代入函数解析式,利用诱导公式化简整理求得答案.
解答:解:∵f(2009)=asin(2009π+α)+bcos(2009π+β)
=asin(π+α)+bcos(π+β)
=-(asinα+bcosβ)=-1,
∴f(2010)=asin(2010π+α)+bcos(2010π+β)
=asinα+bcosβ=1.
故选C
=asin(π+α)+bcos(π+β)
=-(asinα+bcosβ)=-1,
∴f(2010)=asin(2010π+α)+bcos(2010π+β)
=asinα+bcosβ=1.
故选C
点评:本题主要考查了运用诱导公式化简求值的问题.在使用诱导公式的时候注意三角函数的正负值的判定.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
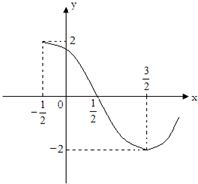 已知f(x)=Asin(ωπx+?)(A>0,ω>0,0<?<π),其导函数f′(x)的部分图象如图所示,则f(0)+f(1)+f(2)+f(3)+…f(2011)的值是( )
已知f(x)=Asin(ωπx+?)(A>0,ω>0,0<?<π),其导函数f′(x)的部分图象如图所示,则f(0)+f(1)+f(2)+f(3)+…f(2011)的值是( )A、-
| ||||
B、
| ||||
| C、1 | ||||
| D、0 |
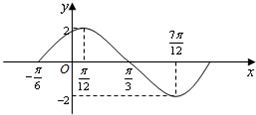 已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示:
已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)图象的一部分如图所示: