题目内容
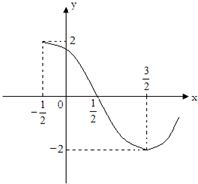已知f（x）=Asin（ωπx+?）（A＞0，ω＞0，0＜?＜π），其导函数f′（x）的部分图象如图所示，则f（0）+f（1）+f（2）+f（3）+…f（2011）的值是（ ）A、-
| ||||
B、
| ||||
| C、1 | ||||
| D、0 |
分析：求出函数的导函数，利用导函数的图象求出A、T、以及?，确定函数的解析式，然后推出f（0），f（1），f（2），f（3），…，f（2011）是以4为周期的周期数列，且f（0）+f（1）+f（2）+f（3）=0得到正确选项．
解答：解：函数f（x）=Asin（ωπx+?）（A＞0，ω＞0，0＜?＜π），其导函数f′（x）=Aωπcos（ωπx+?），
所以Aωπ=2 T=4，所以ωπ=
ω=
A=
因为导数图象过（
，0），所以0=2cos（
+?），所以?=
，
f（x）=
sin（
πx+
），f（0）=
，f（1）=
，f（2）=-
，f（3）=-
，f（4）=
，…
所以f（0），f（1），f（2），f（3），…，f（2011）是以4为周期的周期数列，且f（0）+f（1）+f（2）+f（3）=0，
所以f（0）+f（1）+f（2）+f（3）+…+f（2011）=0
故选D
解：函数f（x）=Asin（ωπx+?）（A＞0，ω＞0，0＜?＜π），其导函数f′（x）=Aωπcos（ωπx+?），所以Aωπ=2 T=4，所以ωπ=
| 2π |
| T |
| 1 |
| 2 |
| 4 |
| π |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
f（x）=
| 4 |
| π |
| 1 |
| 2 |
| π |
| 4 |
| ||
| π |
| ||
| π |
| ||
| π |
| ||
| π |
| ||
| π |
所以f（0），f（1），f（2），f（3），…，f（2011）是以4为周期的周期数列，且f（0）+f（1）+f（2）+f（3）=0，
所以f（0）+f（1）+f（2）+f（3）+…+f（2011）=0
故选D
点评：本题是中档题，考查三角函数的导数的求法，三角函数的解析式的求法，数列的知识，是综合题目，注意图象的信息的应用．
练习册系列答案
相关题目
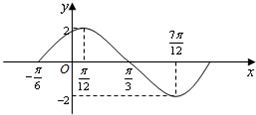已知f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）图象的一部分如图所示：