题目内容
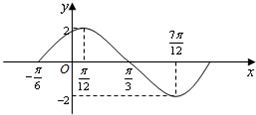已知f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）图象的一部分如图所示：（1）求f（x）的解析式；
（2）写出f（x）的单调区间．
分析：（1）由图象直接求出A和T，可求ω，根据特殊点（
，2）求出φ，即可求函数f（x）的解析式；
（2）根据正弦函数的单调性直接求出函数的单调增区间和单调减区间即可．
| π |
| 12 |
（2）根据正弦函数的单调性直接求出函数的单调增区间和单调减区间即可．
解答：解：（1）由图可知A=2T=π∴ω=2
当x=
时f（x）取最大值∴2×
+φ=
∴φ=
符合条件
∴f（x）=2sin（2x+
）（6分）
（2）f（x）的单调递增区间为[kπ-
，kπ+
] k∈Z（9分）
f（x）的单调递减区间为[kπ+
，kπ+
] k∈Z（12分）
当x=
| π |
| 12 |
| π |
| 12 |
| π |
| 2 |
| π |
| 3 |
∴f（x）=2sin（2x+
| π |
| 3 |
（2）f（x）的单调递增区间为[kπ-
| 5π |
| 12 |
| π |
| 12 |
f（x）的单调递减区间为[kπ+
| π |
| 12 |
| 7π |
| 12 |
点评：本题考查三角函数y=Asin（ωx+φ）的图象及其解析式，三角函数的单调性，考查计算能力，是基础题．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
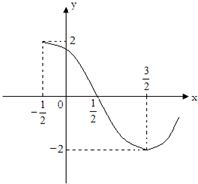已知f（x）=Asin（ωπx+?）（A＞0，ω＞0，0＜?＜π），其导函数f′（x）的部分图象如图所示，则f（0）+f（1）+f（2）+f（3）+…f（2011）的值是（ ）A、-
| ||||
B、
| ||||
| C、1 | ||||
| D、0 |