题目内容
(2012•道里区二模)已知函数f(x)=Msin(ωx+φ)+B(M>0,0<ω<2,|φ|<
)的一系列对应值如下表:
(1)根据表格提供的数据求y=f(x)的解析式;
(2)在△ABC中,角A、B、C的对边分别为a、b、c,cosA=f(
)+
,b=3c,求sinC.
| π |
| 2 |
| x | -
|
|
|
|
|
|
| ||||||||||||||
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(2)在△ABC中,角A、B、C的对边分别为a、b、c,cosA=f(
| π |
| 6 |
| 1 |
| 3 |
分析:(1)通过最大值与最小值,求出M,B,通过函数的周期求出ω,利用函数的图象最低点的坐标,求出φ,即可解出函数f(x)的解析式;
(2)先求出cosA=
,再利用余弦定理,求出
=2
,利用正弦定理可得结论.
(2)先求出cosA=
| 1 |
| 3 |
| a |
| c |
| 2 |
解答:解:(1)由题意,
,∴
∵函数的周期为
-(-
)=2π,∴ω=
=1
∴f(x)=2sin(x-φ)+1
将(-
,-1)代入可得sin(-
-φ)=-1
∵|φ|<
,∴φ=
∴f(x)=2sin(x-
)+1…(4分)
(Ⅱ)∵f(x)=2sin(x-
)+1,∴f(
)=2sin(
-
)+1=0
∵cosA=f(
)+
,∴cosA=
…(6分)
∵b=3c,由余弦定理得a2=b2+c2-2bccosA=8c2…(8分)
∴
=2
∵cosA=
,∴sinA=
∴由正弦定理得
=
,∴sinC=
=
…(12分)
|
|
∵函数的周期为
| 11π |
| 6 |
| π |
| 6 |
| 2π |
| T |
∴f(x)=2sin(x-φ)+1
将(-
| π |
| 6 |
| π |
| 6 |
∵|φ|<
| π |
| 2 |
| π |
| 3 |
∴f(x)=2sin(x-
| π |
| 3 |
(Ⅱ)∵f(x)=2sin(x-
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
∵cosA=f(
| π |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
∵b=3c,由余弦定理得a2=b2+c2-2bccosA=8c2…(8分)
∴
| a |
| c |
| 2 |
∵cosA=
| 1 |
| 3 |
2
| ||
| 3 |
∴由正弦定理得
| a |
| sinA |
| c |
| sinC |
| csinA |
| a |
| 1 |
| 3 |
点评:本题考查学生的读图能力,考查函数解析式的确定,考查余弦、正弦定理的运用,属于中档题.

练习册系列答案
相关题目
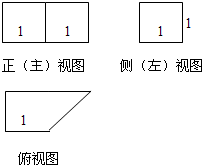 (2012•道里区二模)一个几何体的三视图如图所示,则该几何体的体积为( )
(2012•道里区二模)一个几何体的三视图如图所示,则该几何体的体积为( )