题目内容
(2012•道里区二模)已知△ABC,∠C=60°,AC=2,BC=1,点M是△ABC内部或边界上一动点,N是边BC的中点,则
•
的最大值为
.
| AN |
| AM |
| 7 |
| 2 |
| 7 |
| 2 |
分析:由题意,得△ABC是以B为直角的直角三角形,因此建立如图直角坐标系,设M(x,y),可得向量
和
的坐标,从而得到
•
关于x、y的表达式,结合点M在△ABC内部或边界上运动,可得当点M与原点重合时
•
的最大值为
.
| AM |
| AN |
| AN |
| AM |
| AN |
| AM |
| 7 |
| 2 |
解答:解:∵∠C=60°,AC=2,BC=1,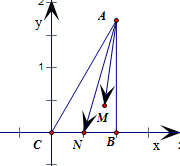
∴AB2=AC2+BC2-2AC•BCcos60°=3,得AB=
可得△ABC是以B为直角的直角三角形
因此,以C为原点,CB所在直线为x轴建立如图坐标系,
可得C(0,0),B(1,0),A(1,
)
∴BC中点N(
,0),得
=(-
,-
)
设M(x,y),得
=(x-1,y-
)
∴
•
=-
(x-1)+(-
)(y-
)=-
x-
y+
点M在△ABC内部或边界上运动,当点M与原点重合时,-
x-
y+
=
,取得最大值
即
•
的最大值为
故答案为:

∴AB2=AC2+BC2-2AC•BCcos60°=3,得AB=
| 3 |
可得△ABC是以B为直角的直角三角形
因此,以C为原点,CB所在直线为x轴建立如图坐标系,
可得C(0,0),B(1,0),A(1,
| 3 |
∴BC中点N(
| 1 |
| 2 |
| AN |
| 1 |
| 2 |
| 3 |
设M(x,y),得
| AM |
| 3 |
∴
| AN |
| AM |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 7 |
| 2 |
点M在△ABC内部或边界上运动,当点M与原点重合时,-
| 1 |
| 2 |
| 3 |
| 7 |
| 2 |
| 7 |
| 2 |
即
| AN |
| AM |
| 7 |
| 2 |
故答案为:
| 7 |
| 2 |
点评:本题给出直角三角形内的动点,求向量数量的最大值,着重考查了解三角形和平面向量的数量积公式等知识,属于中档题.

练习册系列答案
相关题目
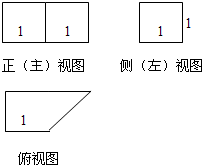 (2012•道里区二模)一个几何体的三视图如图所示,则该几何体的体积为( )
(2012•道里区二模)一个几何体的三视图如图所示,则该几何体的体积为( )