题目内容
【题目】已知函数f(x)=2sinx(sinx+cosx).
(1)求函数的最大值;
(2)求该函数在区间[![]() ]上的单调递增区间.
]上的单调递增区间.
【答案】(1)![]() ;(2)[
;(2)[![]() ,
,![]() ].
].
【解析】
(1)利用二倍角的正弦、余弦公式以及辅助角公式,将函数f(x)化为![]() sin(2x
sin(2x![]() )+1的形式,利用三角函数的性质即可求解.
)+1的形式,利用三角函数的性质即可求解.
(2)利用正弦函数的单调增区间[2kπ![]() ,2kπ
,2kπ![]() ],k∈Z,整体代入即可求解.
],k∈Z,整体代入即可求解.
(1)由题意,
f(x)=2sinx(sinx+cosx)=2sin2x+2sinxcosx
=1﹣cos2x+sin2x
=sin2x﹣cos2x+1
![]() sin(2x
sin(2x![]() )+1.
)+1.
∴函数f(x)的最大值为![]() 1.
1.
(2)由题意,正弦函数的单调递增区间为[2kπ![]() ,2kπ
,2kπ![]() ],k∈Z.
],k∈Z.
则有2kπ![]() 2x
2x![]() 2kπ
2kπ![]() ,k∈Z.
,k∈Z.
化简,得kπ![]() x
x![]() kπ
kπ![]() ,k∈Z.
,k∈Z.
根据题意,![]() x
x![]() ,
,
∴该函数在区间[![]() ]上的单调递增区间为[
]上的单调递增区间为[![]() ,
,![]() ].
].

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
【题目】为降低汽车尾气的排放量,某厂生产甲乙两种不同型号的节排器,分别从甲乙两种节排器中各自抽取100件进行性能质量评估检测,综合得分情况的频率分布直方图如图所示.
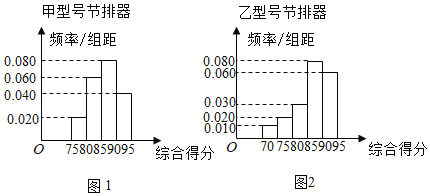
节排器等级及利润如表格表示,其中![]()
综合得分 | 节排器等级 | 节排器利润率 |
| 一级品 |
|
| 二级品 |
|
| 三级品 |
|
(1)若从这100件甲型号节排器按节排器等级分层抽样的方法抽取10件,再从这10件节排器中随机抽取3件,求至少有2件一级品的概率;
(2)视频率分布直方图中的频率为概率,用样本估计总体,则
①若从乙型号节排器中随机抽取3件,求二级品数![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
②从长期来看,骰子哪种型号的节排器平均利润较大?