题目内容
 已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,底面ABCD的对角线的交点为F,AC=2
已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,底面ABCD的对角线的交点为F,AC=2| 2 |
(Ⅰ)证明:PC⊥EF;
(Ⅱ)证明∠BED是二面角B-PC-D的平面角;
(Ⅲ)设二面角A-PB-C为90°,求PD与平面PBC所成角的大小.
分析:(I)证明△FCE∽△PCA,∠FEC=∠PAC=90°,即可得出结论;
(II)证明PC⊥平面BED,可得EB⊥PC,ED⊥PC,从而∠BED是二面角B-PC-D的平面角;
(III)在平面PAB内过点A作AG⊥PB,G为垂足,证明BC⊥平面PAB,求出D点到平面PBC的距离,即可求出PD与平面PBC所成角的大小.
(II)证明PC⊥平面BED,可得EB⊥PC,ED⊥PC,从而∠BED是二面角B-PC-D的平面角;
(III)在平面PAB内过点A作AG⊥PB,G为垂足,证明BC⊥平面PAB,求出D点到平面PBC的距离,即可求出PD与平面PBC所成角的大小.
解答:(Ⅰ)证明:因为AC=2
,PA=2,PE=2EC,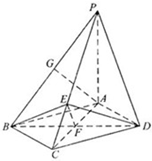
故PC=2
,EC=
,FC=
,
从而
=
,
=
.
因为
=
,∠FCE=∠PCA,
所以△FCE∽△PCA,∠FEC=∠PAC=90°,
由此知PC⊥EF. …(5分)
(Ⅱ)证明:因为底面ABCD为菱形,所以BD⊥AC.
又PA⊥底面ABCD,所以PC⊥BD.
由(Ⅰ)知PC⊥EF,所以PC与平面BED内两条相交直线BD,EF都垂直,
所以PC⊥平面BED.
因为BE、ED在平面平面BED内,所以EB⊥PC,ED⊥PC,所以∠BED是二面角B-PC-D的平面角. …(9分)
(Ⅲ)解:在平面PAB内过点A作AG⊥PB,G为垂足.
因为二面角A-PB-C为90°,所以平面PAB⊥平面PBC.
又平面PAB∩平面PBC=PB.
故AG⊥平面PBC,AG⊥BC.
所以BC与平面PAB内两条相交直线PA,AG都垂直,故BC⊥平面PAB,
于是BC⊥AB,
所以底面ABCD为正方形,AD=2,PD=
=2
. …(11分)
设D到平面PBC的距离为d.
因为AD∥BC,且AD?平面PBC,BC?平面PBC,
故AD∥平面PBC,A、D两点到平面PBC的距离相等,即d=AG=
.
设PD与平面PBC所成的角为α,则sina=
=
.
所以PD与平面PBC所成的角为30°. …(14分)
| 2 |

故PC=2
| 3 |
2
| ||
| 3 |
| 2 |
从而
| PC |
| FC |
| 6 |
| AC |
| EC |
| 6 |
因为
| PC |
| FC |
| AC |
| EC |
所以△FCE∽△PCA,∠FEC=∠PAC=90°,
由此知PC⊥EF. …(5分)
(Ⅱ)证明:因为底面ABCD为菱形,所以BD⊥AC.
又PA⊥底面ABCD,所以PC⊥BD.
由(Ⅰ)知PC⊥EF,所以PC与平面BED内两条相交直线BD,EF都垂直,
所以PC⊥平面BED.
因为BE、ED在平面平面BED内,所以EB⊥PC,ED⊥PC,所以∠BED是二面角B-PC-D的平面角. …(9分)
(Ⅲ)解:在平面PAB内过点A作AG⊥PB,G为垂足.
因为二面角A-PB-C为90°,所以平面PAB⊥平面PBC.
又平面PAB∩平面PBC=PB.
故AG⊥平面PBC,AG⊥BC.
所以BC与平面PAB内两条相交直线PA,AG都垂直,故BC⊥平面PAB,
于是BC⊥AB,
所以底面ABCD为正方形,AD=2,PD=
| PA2+AD2 |
| 2 |
设D到平面PBC的距离为d.
因为AD∥BC,且AD?平面PBC,BC?平面PBC,
故AD∥平面PBC,A、D两点到平面PBC的距离相等,即d=AG=
| 2 |
设PD与平面PBC所成的角为α,则sina=
| d |
| PD |
| 1 |
| 2 |
所以PD与平面PBC所成的角为30°. …(14分)
点评:本题考查线线垂直,考查空间角,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点. 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.