题目内容
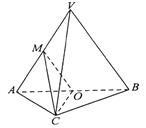
【题目】已知F1(﹣c,0)、F2(c,0)分别是椭圆G: ![]() 的左、右焦点,点M是椭圆上一点,且MF2⊥F1F2 , |MF1|﹣|MF2|=
的左、右焦点,点M是椭圆上一点,且MF2⊥F1F2 , |MF1|﹣|MF2|= ![]() a.
a.
(1)求椭圆G的方程;
(2)若斜率为1的直线l与椭圆G交于A、B两点,以AB为底作等腰三角形,顶点为P(﹣3,2),求△PAB的面积.
【答案】
(1)解:∵|MF1|﹣|MF2|= ![]() a,|MF1|+|MF2|=2a,
a,|MF1|+|MF2|=2a,
∴|MF1|= ![]() ,|MF2|=
,|MF2|= ![]() ,
,
∵MF2⊥F1F2,∴ ![]() .
.
即 ![]() ,则
,则 ![]() ,
,
∵c2=a2﹣4,∴a2=12,
∴椭圆 ![]()
(2)解:设直线l的方程为y=x+m.
由 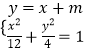 ,得4x2+6mx+3m2﹣12=0.①
,得4x2+6mx+3m2﹣12=0.①
设A、B的坐标分别为(x1,y1)、(x2,y2)(x1<x2),AB的中点为E(x0,y0),
则 ![]() ,
, ![]() .
.
∵AB是等腰△PAB的底边,∴PE⊥AB.
∴PE的斜率 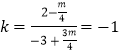 ,解得m=2.
,解得m=2.
此时方程①为4x2+12x=0,解得x1=﹣3,x2=0,∴y1=﹣1,y2=2,
∴|AB|=3 ![]() .
.
此时,点P(﹣3,2)到直线AB:x﹣y+2=0的距离d= ![]() ,
,
∴△PAB的面积S= ![]()
【解析】(1)本题关键是由MF2⊥F1F2得到|MF1|2=|MF2|2+|F1F2|2;(2)设出直线l的方程,借助一元二次方程根与系数的关系表示出PE的斜率,再结合PE⊥AB求得直线l的方程,即可求得三角形PAB的面积.
【考点精析】认真审题,首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() ).
).

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目