Question

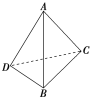
【题目】如图，在三棱锥A-BCD中，AD⊥BD，AC⊥BC，∠DAB＝，∠BAC＝.三棱锥的外接球的表面积为16π，则该三棱锥的体积的最大值为(　　 )

A.B.C.D.

Answer 1

【答案】B

【解析】

设外接球的半径为R，求得R＝2，进而得到三棱锥的外接球的球心为AB的中点，

进而得到三棱锥的体积最大时，平面ADB⊥平面ABC，即可求得三棱锥的体积，得到答案．

由题意得，设外接球的半径为R，因为4πR2＝16π，解得R＝2，

又由都是直角三角形，所以三棱锥的外接球的球心为AB的中点，

且AB＝4.由∠DAB＝，∠BAC＝，可求得AD＝2，BD＝2，AC＝BC＝2，

当三棱锥的体积最大时，平面ADB⊥平面ABC，

所以三棱锥的体积的最大值为××2×2 ×2＝.

故选：B.