题目内容
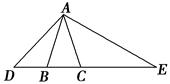
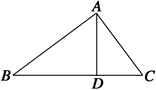
在Rt△ABC中,∠BAC=90°,AD⊥BC,垂足为D.若BC=m,∠B=α,则AD的长为
A.m sin2α B.m cos2α
C.m sin αcos α D.m sin αtan α
A.m sin2α B.m cos2α
C.m sin αcos α D.m sin αtan α
C
由射影定理,得AB2=BD·BC,AC2=CD·BC,
即m2cos2α=BD·m,m2sin2α=CD·m,
即BD=mcos2α,CD=msin2α.
又∵AD2=BD·DC=m2cos2αsin2α,
∴AD=mcos αsin α.故选C.
即m2cos2α=BD·m,m2sin2α=CD·m,
即BD=mcos2α,CD=msin2α.
又∵AD2=BD·DC=m2cos2αsin2α,
∴AD=mcos αsin α.故选C.

练习册系列答案
相关题目
 ,则B′C′=________.
,则B′C′=________.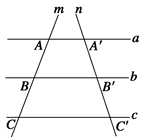
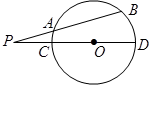
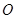 的割线
的割线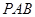 交圆
交圆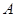 、
、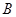 两点,割线
两点,割线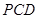 经过圆心.已知
经过圆心.已知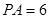 ,
,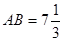 ,
,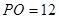 .则圆
.则圆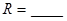 .
.