题目内容
已知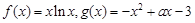 .
.
(1) 求函数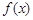 在
在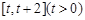 上的最小值;
上的最小值;
(2) 对一切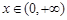 ,
,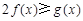 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3) 证明:对一切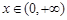 ,都有
,都有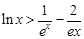 成立.
成立.
【答案】
(1) (2)
(2)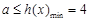
(3)构造函数 ,则
,则 ,
,
设 ,则
,则 ,
,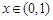 ,利用单调性来得到证明。
,利用单调性来得到证明。
【解析】
试题分析:(1)  ,当
,当 ,
, ,
, 单调递减,当
单调递减,当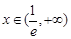 ,
, ,
, 单调递增.
单调递增.
①  ,t无解;
,t无解;
② 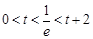 ,即
,即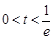 时,
时, ;
;
③  ,即
,即 时,
时, 在
在 上单调递增,
上单调递增, ;
;
所以 .
.
(2)  ,则
,则 ,
,
设 ,则
,则 ,
,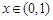 ,
, ,
,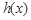 单调递减,
单调递减, ,
, ,
,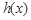 单调递增,所以
单调递增,所以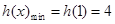 .
.
因为对一切 ,
, 恒成立,所以
恒成立,所以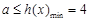
(3)
问题等价于证明 ,由⑴可知
,由⑴可知 的
的
最小值是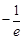 ,当且仅当
,当且仅当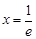 时取到
时取到
设 ,则
,则 ,易得
,易得 ,当且仅当
,当且仅当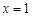 时取到,从而对一切
时取到,从而对一切 ,都有
,都有 成立.
成立.
考点:导数的运用
点评:主要是考查了导数在研究函数中的运用,求解单调性以及极值和最值,属于基础题。

练习册系列答案
相关题目
要解决下面四个问题,只用顺序结构画不出其程序框图的是( )
A、利用1+2+…+n=
| ||
| B、当图面积已知时,求圆的周长 | ||
| C、当给定一个数x,求其绝对值 | ||
| D、求函数f(x)=x2-4x+5的函数值 |
 .
. 的最小正周期;
的最小正周期; 上的函数值的取值范围.
上的函数值的取值范围. .
. 的最小正周期;
的最小正周期; 上的函数值的取值范围.
上的函数值的取值范围. .
. 的最小正周期;
的最小正周期;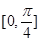 上的函数值的取值范围.
上的函数值的取值范围. ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______. 、…、
、…、 、
、 可一般表示为
可一般表示为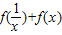 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题: ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.