题目内容
问题1:已知函数 ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______.我们若把每一个函数值计算出,再求和,对函数值个数较少时是常用方法,但函数值个数较多时,运算就较繁锁.观察和式,我们发现
 、…、
、…、 、
、 可一般表示为
可一般表示为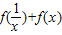 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:问题2:已知函数
 ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
【答案】分析:问题1:根据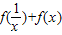 =
=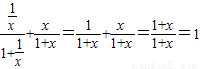 为定值,从而所求式子分组求和可求;
为定值,从而所求式子分组求和可求;
问题2:先研究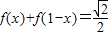 ,再分组求和可求.
,再分组求和可求.
解答:解:问题1:∵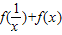 =
=
∴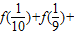 …
… …+f(9)+f(10)=9+
…+f(9)+f(10)=9+ =
=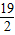 (4分)
(4分)
问题2: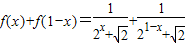 =
=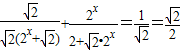 (10分)
(10分)
f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)
=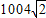 (14分)
(14分)
点评:本题的考点是类比推理,关键是理解问题1,发现解决问题的规律,从而得解.
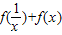 =
=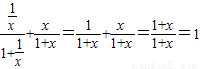 为定值,从而所求式子分组求和可求;
为定值,从而所求式子分组求和可求;问题2:先研究
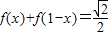 ,再分组求和可求.
,再分组求和可求.解答:解:问题1:∵
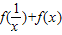 =
=
∴
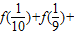 …
… …+f(9)+f(10)=9+
…+f(9)+f(10)=9+ =
=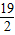 (4分)
(4分)问题2:
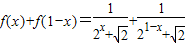 =
=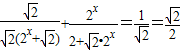 (10分)
(10分)f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)
=
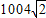 (14分)
(14分)点评:本题的考点是类比推理,关键是理解问题1,发现解决问题的规律,从而得解.

练习册系列答案
相关题目
 ,则
,则 …
… …+f(9)+f(10)=______.
…+f(9)+f(10)=______. 、…、
、…、 、
、 可一般表示为
可一般表示为 =
= 为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题:
为定值,有此规律从而很方便求和,请求出上述结果,并用此方法求解下面问题: ,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.
,求f(-2007)+f(-2006)+…+f(-1)+f(0)+f(1)+…+f(2007)+f(2008)的值.