题目内容
【题目】已知单调递增的等比数列{an}满足a2+a3+a4=28，且a3+2是a2 ， a4的等差中项．
（1）求数列{an}的通项公式；
（2）设bn=anlog2an ， 其前n项和为Sn ， 若（n﹣1）2≤m（Sn﹣n﹣1）对于n≥2恒成立，求实数m的取值范围．
【答案】
（1）解：设等比数列的{an}首项为a1，公比为q．
由题意可知：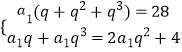 
，
解得：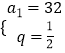 
或 
，
∵数列为单调递增的等比数列，
∴an=2n；
（2）解：bn=anlog2an=n2n，
∴Sn=b1+b2+…+bn=121+222+…+n2n，①
2Sn=122+223+324+…+n2n+1，②
①﹣②，得：﹣Sn=2+22+23+…+2n﹣n2n+1
= 
﹣n2n+1=2n+1﹣2﹣n2n+1，
∴Sn=（n﹣1）2n+1+2，
若（n﹣1）2≤m（Sn﹣n﹣1）对于n≥2恒成立，
则（n﹣1）2≤m[（n﹣1）2n+1+2﹣n﹣1]=m[（n﹣1）2n+1+1﹣n]对于n≥2恒成立，
即 
= 
对于n≥2恒成立，
∵ 
= 
，
∴数列{ }为递减数列，
则当n=2时， 的最大值为 
．
∴m≥ ．
则实数m得取值范围为[ ，+∞）．
【解析】（1）设出等比数列{an}的首项和公比，由已知列式求得首项和公比，则数列{an}的通项公式可求；（2）把（1）中求得的通项公式代入bn=anlog2an ， 利用错位相减法求得Sn ， 代入（n﹣1）2≤m（Sn﹣n﹣1），分离变量m，由单调性求得最值得答案．
【考点精析】本题主要考查了对数的运算性质和数列的前n项和的相关知识点，需要掌握①加法：
②减法：
③数乘：
④
⑤
；数列{an}的前n项和sn与通项an的关系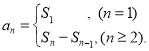
才能正确解答此题．
练习册系列答案
相关题目
