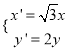题目内容
【题目】已知△ABC的两个顶点A,B的坐标分别为(﹣2,0),(2,0),且AC,BC所在直线的斜率之积等于![]() .
.
(1)求顶点C的轨迹方程;
(2)若斜率为1的直线![]() 与顶点C的轨迹交于M,N两点,且|MN|=
与顶点C的轨迹交于M,N两点,且|MN|=![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(Ⅰ)![]() (Ⅱ)y=x±1
(Ⅱ)y=x±1
【解析】
试题(Ⅰ)设出C的坐标,利用AC、BC所在直线的斜率之积等于﹣![]() ,列出方程,求出点C的轨迹方程;
,列出方程,求出点C的轨迹方程;
(Ⅱ)设直线l的方程为y=x+m,与椭圆方程联立,利用韦达定理,结合|MN|=![]() ,即可求直线l的方程.
,即可求直线l的方程.
解:(Ⅰ)设C的坐标为(x,y),则
直线AC的斜率![]() ,
,
直线BC的斜率![]() ,
,
由已知有![]() ,化简得顶点C的轨迹方程,
,化简得顶点C的轨迹方程,![]()
(Ⅱ)设直线l的方程为y=x+m,M(x1,y1),N(x2,y2),
由题意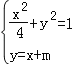 ,解得5x2+8mx+4m2﹣4=0,
,解得5x2+8mx+4m2﹣4=0,
△=64m2﹣20(4m2﹣4)>0,解得![]()
∴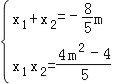 ,
,![]()
代入解得m2=1,m=±1,
∴直线l的方程为y=x±1.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
【题目】某高级中学今年高一年级招收“国际班”学生![]() 人,学校为这些学生开辟了直升海外一流大学的绿色通道,为了逐步提高这些学生与国际教育接轨的能力,将这
人,学校为这些学生开辟了直升海外一流大学的绿色通道,为了逐步提高这些学生与国际教育接轨的能力,将这![]() 人分为三个批次参加国际教育研修培训,在这三个批次的学生中男、女学生人数如下表:
人分为三个批次参加国际教育研修培训,在这三个批次的学生中男、女学生人数如下表:
第一批次 | 第二批次 | 第三批次 | |
女 |
|
|
|
男 |
|
|
|
已知在这![]() 名学生中随机抽取
名学生中随机抽取![]() 名,抽到第一批次、第二批次中女学生的概率分别是
名,抽到第一批次、第二批次中女学生的概率分别是![]() .
.
(1)求![]() 的值;
的值;
(2)为了检验研修的效果,现从三个批次中按分层抽样的方法抽取![]() 名同学问卷调查,则三个批次被选取的人数分别是多少?
名同学问卷调查,则三个批次被选取的人数分别是多少?
(3)若从第(2)小问选取的学生中随机选出两名学生进行访谈,求“参加访谈的两名同学至少有一个人来自第一批次”的概率.