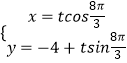题目内容
【题目】当|a|≤1,|x|≤1时,关于x的不等式|x2﹣ax﹣a2|≤m恒成立,则实数m的取值范围是( )
A.[![]() , +∞)
, +∞)
B.[![]() , +∞)
, +∞)
C.[![]() , +∞)
, +∞)
D.[![]() , +∞)
, +∞)
【答案】B
【解析】解:|x2﹣ax﹣a2|=|﹣x2+ax+a2|≤|﹣x2+ax|+|a2|=|﹣x2+ax|+a2 ,
当且仅当﹣x2+ax与a2同号时取等号,
故当﹣x2+ax≥0,有|x2﹣ax﹣a2|=﹣![]() +
+![]() a2 ,
a2 ,
当x=![]() 时,取到最大值
时,取到最大值![]() a2 , 而|a|≤1,|x|≤1,
a2 , 而|a|≤1,|x|≤1,
∴当a=1,x=![]() 或a=﹣1,x=﹣
或a=﹣1,x=﹣![]() 时,
时,
|x2﹣ax﹣a2|有最大值![]() ,
,
故m≥![]() ,
,
故选:B.
【考点精析】认真审题,首先需要了解绝对值不等式的解法(含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号).

练习册系列答案
相关题目