题目内容
10.已知向量$\overrightarrow{a}$=(2sinx,cosx),$\overrightarrow{b}$=($\sqrt{3}$cosx,2cosx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$+m的最大值为2(1)求实数m的值;
(2)求f(x)的递减区间.
分析 (1)利用平面向量数量积的运算及三角函数恒等变换可求函数解析式f(x)=2sin(2x+$\frac{π}{6}$)+m+1,利用正弦函数的有界性即可得解.
(2)根据正弦函数的图象和性质即可求得f(x)的递减区间.
解答 解:(1)∵f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$+m=2$\sqrt{3}$sinxcosx+2cos2x+m=$\sqrt{3}$sin2x+cos2x+1+m=2sin(2x+$\frac{π}{6}$)+m+1,
∴由题意可得:2=2+m+1,解得:m=-1.
(2)∵由(1)可得:f(x)=2sin(2x+$\frac{π}{6}$),
∴由2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ$+\frac{3π}{2}$,k∈Z可解得f(x)的递减区间为:[kπ$+\frac{π}{6}$,k$π+\frac{2π}{3}$],k∈Z.
点评 本题考查了三角函数的单调性、数量积运算性质,考查了正弦函数的图象和性质,三角函数恒等变换的应用,考查了计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.圆台的上、下底面面积分别为4和16,中截面把圆台分成两部分,则这两部分的体积之比为( )
| A. | 37:8 | B. | 8:27 | C. | 27:64 | D. | 19:37 |
18.在△ABC中,余弦定理表达正确的是( )
| A. | a2=b2+c2+2accosA | B. | b2=a2+c2-2accosB | ||
| C. | c2=a2+b2-2absinC | D. | 以上结果都不正确 |
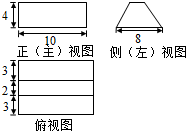 某几何体的三视图如图所示.则该几何体的体积为200.
某几何体的三视图如图所示.则该几何体的体积为200.