题目内容
已知函数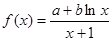 在点
在点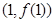 处的切线方程为
处的切线方程为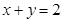 .
.
(I)求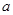 ,
,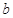 的值;
的值;
(II)对函数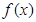 定义域内的任一个实数
定义域内的任一个实数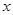 ,
,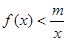 恒成立,求实数
恒成立,求实数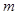 的取值范围.
的取值范围.
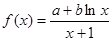 在点
在点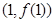 处的切线方程为
处的切线方程为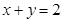 .
.(I)求
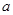 ,
,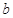 的值;
的值;(II)对函数
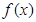 定义域内的任一个实数
定义域内的任一个实数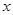 ,
,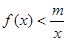 恒成立,求实数
恒成立,求实数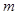 的取值范围.
的取值范围.(I)2,-1(II)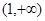
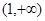
试题分析:(Ⅰ)由
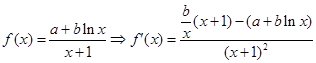
而点
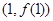 在直线
在直线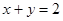 上
上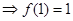 ,又直线
,又直线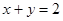 的斜率为
的斜率为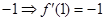
故有
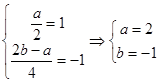
(Ⅱ)由(Ⅰ)得
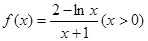
由
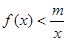 及
及
令
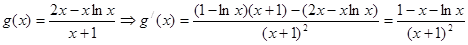
令
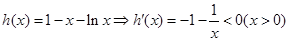 ,故
,故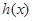 在区间
在区间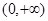 上是减函数,故当
上是减函数,故当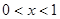 时,
时,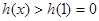 ,当
,当 时,
时,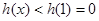
从而当
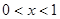 时,
时,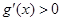 ,当
,当 时,
时,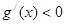
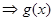 在
在 是增函数,在
是增函数,在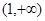 是减函数,故
是减函数,故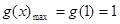
要使
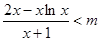 成立,只需
成立,只需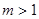
故
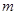 的取值范围是
的取值范围是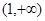 。
。 点评:直线与函数曲线相切时,常从切点入手寻找关系式,充分利用导数的几何意义:函数在某一点处的导数值等于该点处的切线斜率来实现数与形的结合,第二问中将不等式恒成立问题常转化为求函数最值问题,进而借助于导数工具求解

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
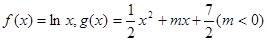 ,直线
,直线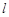 与函数
与函数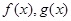 的图像都相切,且与函数
的图像都相切,且与函数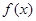 的图像的切点的横坐标为1.
的图像的切点的横坐标为1. 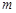 的值;
的值;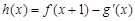 (其中
(其中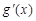 是
是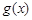 的导函数),求函数
的导函数),求函数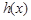 的最大值;
的最大值;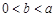 时,求证:
时,求证: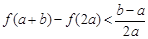 .
.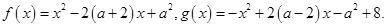 设
设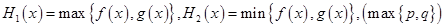 表示
表示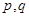 中的较大值,
中的较大值,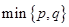 表示
表示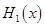 得最小值为
得最小值为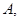
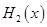 得最小值为
得最小值为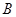 ,则
,则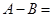 ( )
( )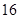
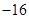
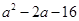
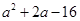
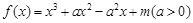 若对任意的
若对任意的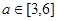 ,不等式
,不等式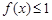 在
在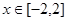 上恒成立,则
上恒成立,则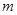 的取值范围是____________.
的取值范围是____________.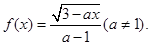
 的定义域是 ;
的定义域是 ; 上是减函数,则实数a的取值范围是 .
上是减函数,则实数a的取值范围是 . 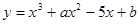 在
在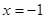 处取得极值
处取得极值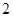 .
.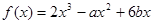 在
在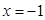 处有极大值7.
处有极大值7.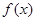 的解析式;(Ⅱ)求
的解析式;(Ⅱ)求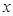 =1处的切线方程.
=1处的切线方程.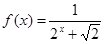 ,利用课本中推导等差数列前n项和公式的方法,可求得
,利用课本中推导等差数列前n项和公式的方法,可求得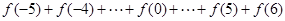 的值 。
的值 。