题目内容
(本小题共12分) 在平面直角坐标系中,已知An(n,an)、Bn(n,bn)、Cn(n-1,0)(n∈N*),满足向量![]() 与向量
与向量![]() 共线,且点An(n,an) (n∈N*)都在斜率为2的同一条直线l上. 若
共线,且点An(n,an) (n∈N*)都在斜率为2的同一条直线l上. 若![]() a1=-3,b1=10
a1=-3,b1=10![]() (1)求数列{an}与{ bn }的通项公式;
(1)求数列{an}与{ bn }的通项公式;
(2)求当n取何值时△AnBnCn的面积Sn最小,并求出Sn的这个最小值。
(Ⅰ) bn= n2-6n+15 (Ⅱ) n=4 Sn的最小值为2
解析:
(1)∵点An(n,an) (n∈N*)都在斜率为2的同一条直线上,[来源:学§科§网Z§X§X§K]
∴![]()
![]() =2,即an+1-an=2,
=2,即an+1-an=2,
于是数列{an}是公差为2的等差数列,又a1=-3,故an= -3+2(n-1)=2n-5.
∵![]() 共线.
共线.
∴1×(-an)-(-1)(bn+1 - bn )=0,即bn+1-bn=an
∴当n≥2时,bn=b1+(b2-b1)+(b3-b2)+ …+(bn-bn-1)
=b1+a1+a2+a3+…+an-1
=10+ (n-1)(n-5)=n2-6n+15
当n=1时,上式也成立.。 所以bn= n2-6n+15
(2)显然,直线AnBn⊥x轴,点Cn到直线AnBn的距离等于1.
所以Sn=![]() [来源:Zxxk.Com]
[来源:Zxxk.Com]
∴当n=4时,Sn取最小值,Sn的最小值为2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ⊥平面
⊥平面 ,
, ∥
∥ 是正三角形,
是正三角形, ,且
,且 是
是 的中点
的中点
 ∥平面
∥平面 ;
; .
. 名,女同学有
名,女同学有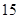 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个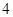 人的课外兴趣小组.
人的课外兴趣小组. 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;


 ,
, ,求证:
,求证: .
. 的值.
的值.