题目内容
已知双曲线与椭圆
+
=1有相同的焦点,它的一条渐近线为y=2x,求双曲线标准方程.
| x2 |
| 9 |
| y2 |
| 4 |
分析:先根据渐近线为y=2x设双曲线方程为x2-
=λ(λ>0),再化成双曲线标准方程得到a,b的值,最后结合双曲线与椭圆
+
=1有相同的焦点得出关于λ的方程,解之可得λ,从而得到双曲线的方程.
| y2 |
| 4 |
| x2 |
| 9 |
| y2 |
| 4 |
解答:解:设双曲线方程为x2-
=λ(λ>0),
则
-
=1(4分),
又椭圆
+
=1的半焦距为
,
根据题意,得λ+4λ=5,解得λ=1,
所以双曲线方程为x2-
=1(9分)
| y2 |
| 4 |
则
| x2 |
| λ |
| y2 |
| 4λ |
又椭圆
| x2 |
| 9 |
| y2 |
| 4 |
| 5 |
根据题意,得λ+4λ=5,解得λ=1,
所以双曲线方程为x2-
| y2 |
| 4 |
点评:本题主要考查圆锥曲线的基本元素之间的关系问题,同时双曲线、椭圆的相应知识也进行了综合性考查.解答的关键是弄清它们的不同点列出方程式求解.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
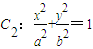 有公共焦点F1F2,点
有公共焦点F1F2,点 是它们的一个公共点.
是它们的一个公共点.