题目内容
已知双曲线与椭圆x2+4y2=64共焦点,它的一条渐近线方程为x-![]() =0,求双曲线的方程.
=0,求双曲线的方程.
答案:
解析:
解析:
解法一:由于双曲线的一条渐近线方程为x-![]() =0,则另一条为x+
=0,则另一条为x+![]() =0.可设双曲线方程为
=0.可设双曲线方程为
x2-3y2=λ(λ>0)即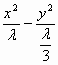 =1,
=1,
由椭圆方程![]() =1可知,
=1可知,
c2=a2-b2=64-16=48,
双曲线与椭圆共焦点,则![]() =48,
=48,
∴λ=36.
故所求双曲线方程为![]() =1.
=1.
解法二:双曲线与椭圆共焦点,可设双曲线方
![]() =1,
=1,
由渐近线方程y=![]() 可得
可得
![]() ,∴λ=28,
,∴λ=28,
故所求双曲线方程为![]() =1.
=1.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
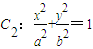 有公共焦点F1F2,点
有公共焦点F1F2,点 是它们的一个公共点.
是它们的一个公共点.