题目内容
已知双曲线C1:x2-y2=m(m>0)与椭圆C2:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(1)求C1,C2的方程;
(2)过点F2且互相垂直的直线l1,l2与圆M:x2+(y+1)2=4分别相交于点A,B和C,D,求|AB|+|CD|的最大值,并求此时直线l1的方程.
分析:(1)把点N(
,1)代入双曲线C1:x2-y2=m(m>0),求得m的值,求得椭圆的焦点,把点N(
,1)代入椭圆C2:
+
=1,解方程组即可求得C1,C2的方程;
(2)根据直线l1,l2与圆相交,由垂径定理可得四边形MEF2F是矩形(其中M是圆的圆心),设圆M的圆心为M,l1、l2被圆M所截得弦的中点分别为E,F,弦长分别为d1,d2,利用勾股定理可得ME2+MF2=F2M2=3,利用基本不等式即可求得|AB|+|CD|的最大值,和此时直线l1的方程.
| 2 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
(2)根据直线l1,l2与圆相交,由垂径定理可得四边形MEF2F是矩形(其中M是圆的圆心),设圆M的圆心为M,l1、l2被圆M所截得弦的中点分别为E,F,弦长分别为d1,d2,利用勾股定理可得ME2+MF2=F2M2=3,利用基本不等式即可求得|AB|+|CD|的最大值,和此时直线l1的方程.
解答:解:(1)点N(
,1)是双曲线C1:x2-y2=m(m>0)上的点,∴m=(
)2-1=1.
∴双曲线C1:x2-y2=1,从而F1(-
,0),F2(
,0),∴a2>b2,且a2-b2=2.①
又点N(
,1)在椭圆上,则
+
=1②
由①②得a2=4,b2=2,所以椭圆的方程为
+
=1.
(2)设圆M的圆心为M,l1、l2被圆M所截得弦的中点分别为E,F,弦长分别为d1,d2,因为四边形MEF2F是矩形,
所以ME2+MF2=F2M2=3,即[4-(
)2]+[4-(
)2]=3,
化简得d12+d22=20
从而d1+d2≤
•
=2
,等号成立?d1=d2=
,
d1=d2=
时,∴(d1+d2)max=2
,
即l1、l2被圆C所截得弦长之和的最大值为2
.
设直线l1的方程为y=k(x-
)
圆心M到直线l1为的距离
,
∴
=
,解得k=4
±
,
∴直线l1的方程为y=4
±
(x-
).
| 2 |
| 2 |
∴双曲线C1:x2-y2=1,从而F1(-
| 2 |
| 2 |
又点N(
| 2 |
| 2 |
| a2 |
| 1 |
| b2 |
由①②得a2=4,b2=2,所以椭圆的方程为
| x2 |
| 4 |
| y2 |
| 2 |
(2)设圆M的圆心为M,l1、l2被圆M所截得弦的中点分别为E,F,弦长分别为d1,d2,因为四边形MEF2F是矩形,
所以ME2+MF2=F2M2=3,即[4-(
| d1 |
| 2 |
| d2 |
| 2 |
化简得d12+d22=20
从而d1+d2≤
| 2 |
|
| 10 |
| 10 |
d1=d2=
| 10 |
| 10 |
即l1、l2被圆C所截得弦长之和的最大值为2
| 10 |
设直线l1的方程为y=k(x-
| 2 |
圆心M到直线l1为的距离
|
∴
|
| ||
|
|
| 2 |
| 33 |
∴直线l1的方程为y=4
| 2 |
| 33 |
| 2 |
点评:此题是个难题.本题考查了椭圆的定义、离心率、椭圆与双曲线的标准方程及简单的几何性质、直线与圆的位置关系,是一道综合性的试题,考查了学生综合运用知识解决问题的能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
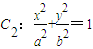 有公共焦点F1F2,点
有公共焦点F1F2,点 是它们的一个公共点.
是它们的一个公共点.