题目内容
把一颗骰子投掷两次,观察出现的点数,并记第一次出现的点数为a,第二次出现的
点数为b,向量 =(-1,-2),
=(-1,-2),
①,若向量 =(-a,b),求当
=(-a,b),求当 ⊥
⊥ 时的慨率;
时的慨率;
②,若向量 =(a,b),又
=(a,b),又 ∥
∥ ,且
,且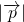 =2
=2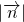 时,求向量
时,求向量 的坐标.
的坐标.
解:①由题意知本题是一个等可能事件的概率,
试验发生包含的事件是点数对(a,b)共有6×6=36对,
满足条件的事件是 ⊥
⊥ 得a-2b=0,即a=2b,
得a-2b=0,即a=2b,
∴数对(a,b)只有三对:(1,2)、(2,4)、(3,6),
∴向量 =(-1,2)、(-2,4)、(-3,6)只有3个,
=(-1,2)、(-2,4)、(-3,6)只有3个,
此时的慨率P=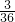 =
= ;
;
②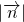 =
= ,
,
∴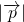 =
= =2
=2 ,a2+b2=20,
,a2+b2=20,
又 ∥
∥ ,
,
∴b=2a,得a2=4,
∴a=2,b=4,
∴向量 =(2,4)
=(2,4)
分析:①本题是一个等可能事件的概率,试验发生包含的事件是点数对(a,b)共有6×6对,满足条件的事件是 ⊥
⊥ 得a-2b=0,即a=2b,列举出所有的满足条件的事件,根据等可能事件的概率得到结果.
得a-2b=0,即a=2b,列举出所有的满足条件的事件,根据等可能事件的概率得到结果.
②根据所给的条件,列出向量平行和向量的模长的关系式,得到两个关于a,b的方程,根据方程组解出a,b的值,得到要求的概率.
点评:本题考查等可能事件的概率,考查向量的模长和向量平行的充要条件,是一个综合题目,题目涉及到向量的运算,使得运算过程中数子比较杂,不要在数字上出错.
试验发生包含的事件是点数对(a,b)共有6×6=36对,
满足条件的事件是
 ⊥
⊥ 得a-2b=0,即a=2b,
得a-2b=0,即a=2b,∴数对(a,b)只有三对:(1,2)、(2,4)、(3,6),
∴向量
 =(-1,2)、(-2,4)、(-3,6)只有3个,
=(-1,2)、(-2,4)、(-3,6)只有3个,此时的慨率P=
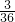 =
= ;
;②
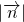 =
= ,
,∴
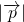 =
= =2
=2 ,a2+b2=20,
,a2+b2=20,又
 ∥
∥ ,
,∴b=2a,得a2=4,
∴a=2,b=4,
∴向量
 =(2,4)
=(2,4)分析:①本题是一个等可能事件的概率,试验发生包含的事件是点数对(a,b)共有6×6对,满足条件的事件是
 ⊥
⊥ 得a-2b=0,即a=2b,列举出所有的满足条件的事件,根据等可能事件的概率得到结果.
得a-2b=0,即a=2b,列举出所有的满足条件的事件,根据等可能事件的概率得到结果.②根据所给的条件,列出向量平行和向量的模长的关系式,得到两个关于a,b的方程,根据方程组解出a,b的值,得到要求的概率.
点评:本题考查等可能事件的概率,考查向量的模长和向量平行的充要条件,是一个综合题目,题目涉及到向量的运算,使得运算过程中数子比较杂,不要在数字上出错.

练习册系列答案
相关题目
(文)把一颗骰子投掷两次,第一次出现的点数记为a,第二次出现的点数记为b.已知直线l1:x+2y=2,直线l2:ax+by=4,则两直线l1、l2平行的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|