题目内容
已知向量| m |
| n |
(1)当x为何值时,
| m |
| n |
(2)解关于x的不等式|
| m |
| n |
| m |
| n |
分析:(1)利用向量垂直的充要条件列出方程,解方程求出x的值.
(2)利用向量模的平方等于向量的平方,将已知不等式平方展开,得到指数不等式;讨论底数与1的大小;利用指数函数的单调性求出解集.
(2)利用向量模的平方等于向量的平方,将已知不等式平方展开,得到指数不等式;讨论底数与1的大小;利用指数函数的单调性求出解集.
解答:解:(1)因为
⊥
,所以
•
=0,(2分)
得a2x-a2=0,即a2x=a2.(4分)
所以2x=2,即x=1,∴当x=1时,
⊥
.(6分)
(2)∵|
+
|<|
-
|,∴(
+
)2<(
-
)2,∴
•
<0.
所以a2x-a2<0,即a2x<a2.(10分)
当0<a<1时,x>1,当a>1时,x<1.
综上,当0<a<1时,不等式的解集为(1,+∞);
当a>1时,不等式的解集为(-∞,1).(14分)
| m |
| n |
| m |
| n |
得a2x-a2=0,即a2x=a2.(4分)
所以2x=2,即x=1,∴当x=1时,
| m |
| n |
(2)∵|
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
所以a2x-a2<0,即a2x<a2.(10分)
当0<a<1时,x>1,当a>1时,x<1.
综上,当0<a<1时,不等式的解集为(1,+∞);
当a>1时,不等式的解集为(-∞,1).(14分)
点评:本题考查向量垂直的充要条件、考查向量模的性质:模的平方等于向量的平方、考查指数函数的单调性与底数与1的大小有关.

练习册系列答案
相关题目
 ,1),则函数图象上过点P的切线斜率等于
,1),则函数图象上过点P的切线斜率等于
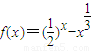 在区间(0,1)上存在零点.
在区间(0,1)上存在零点. 与向量
与向量 的夹角为锐角,那么实数m的取值范围是(
的夹角为锐角,那么实数m的取值范围是( )
)