题目内容
(2012•芜湖二模)给出以下五个命题:
①命题“?x∈R,x2+x+1>0”的否定是:“?x∈R,x2+x+1<0”.
②已知函数f(x)=k•cosx的图象经过点P(
,1),则函数图象上过点P的切线斜率等于-
③a=1是直线y=ax+1和直线y=(a-2)x-1垂直的充要条件.
④函数f(x)=(
)x-x
在区间(0,1)上存在零点.
⑤已知向量
=(1,-2)与向量
=(1,m)的夹角为锐角,那么实数m的取值范围是(-∞,
)
其中正确命题的序号是
①命题“?x∈R,x2+x+1>0”的否定是:“?x∈R,x2+x+1<0”.
②已知函数f(x)=k•cosx的图象经过点P(
| π |
| 3 |
| 3 |
③a=1是直线y=ax+1和直线y=(a-2)x-1垂直的充要条件.
④函数f(x)=(
| 1 |
| 2 |
| 1 |
| 3 |
⑤已知向量
| a |
| b |
| 1 |
| 2 |
其中正确命题的序号是
②③④
②③④
.分析:根据全称、特称命题的否定方法,可判断①的真假;
根据已知求出k值,进而求出导数解析式,代入点的横坐标,可判断②的真假;
根据直线垂直的充要条件,可斜率积为-1,可判断③的真假;
根据零点存在定理可得④的真假
根据m=-2时两向量同向,夹角为0,可判断⑤的真假
根据已知求出k值,进而求出导数解析式,代入点的横坐标,可判断②的真假;
根据直线垂直的充要条件,可斜率积为-1,可判断③的真假;
根据零点存在定理可得④的真假
根据m=-2时两向量同向,夹角为0,可判断⑤的真假
解答:解:①错,命题“?x∈R,x2+x+1>0”的否定是:“?x∈R,x2+x+1≤0”.
②中k•cos
=1,∴k=2,∴f(x)=2cosx,∴f'(x)=-2sinx斜率f′(
)=-2sin
=-
正确
③正确,a=1时,直线y=ax+1和直线y=(a-2)x-1垂直成立,直线y=ax+1和直线y=(a-2)x-1垂直时,斜率积为-1,则
a=1④中f(0)=1>0,f(1)=
-1<0∴有零点,正确
⑤错,m≠-2,当m=-2时两向量同向
故答案为:②③④
②中k•cos
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
③正确,a=1时,直线y=ax+1和直线y=(a-2)x-1垂直成立,直线y=ax+1和直线y=(a-2)x-1垂直时,斜率积为-1,则
a=1④中f(0)=1>0,f(1)=
| 1 |
| 2 |
⑤错,m≠-2,当m=-2时两向量同向
故答案为:②③④
点评:本题考查的知识点是命题的真假判断,熟练掌握相关的基本概念是关键.

练习册系列答案
相关题目
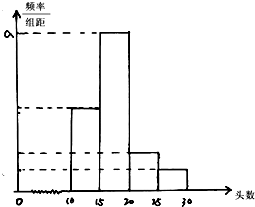 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: