题目内容
(本小题满分14分)已知定义在实数集上的函数fn(x)=xn,n∈N*,其导函数记为 ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
(1)试求a的值;
(2)记函数
 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值;
(3)对于(2)中的b,设函数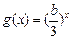 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.
 ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.(1)试求a的值;
(2)记函数

 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值;(3)对于(2)中的b,设函数
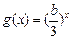 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.解:(1) ,
,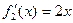 , ………1分
, ………1分
依题意,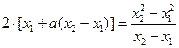 ,得,
,得, . ………3分
. ………3分
(2)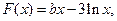
 ,
,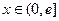 , ………4分
, ………4分
①若 ,
, ,
,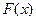 在
在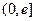 上单调递减,
上单调递减,
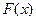 的最小值是
的最小值是 ,由
,由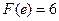 得,
得,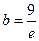 (舍去); ………6分
(舍去); ………6分
②若 ,
,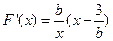 ,令
,令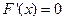 得
得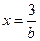 ,
,
当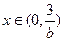 时,
时,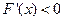 ,
,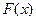 在
在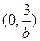 上单调递减;
上单调递减;
当 时,
时,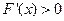 ,
,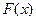 在
在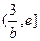 上单调递增;
上单调递增;
所以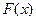 的最小值是
的最小值是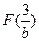 ,由
,由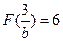 得,
得,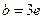 . ………8分
. ………8分
(3)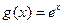 ,结合图象猜测
,结合图象猜测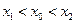 .………9分
.………9分
只需证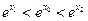 ,∵
,∵ ,
,
故只需证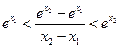 ,
,
即证: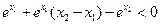 ,且
,且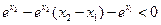 , ………10分
, ………10分
设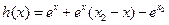 ,
,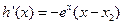 ,当
,当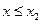 时,
时, ,
,
∴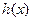 在
在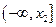 上是增函数,
上是增函数,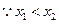 ,∴
,∴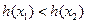 ,而
,而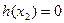
即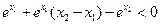 , ………12分
, ………12分
设 ,则
,则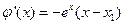 ,当
,当 时,
时,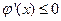 ,
,
∴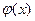 在
在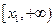 上是减函数,
上是减函数,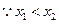 ,∴
,∴ ,而
,而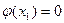
即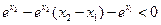 .综上所述,
.综上所述, 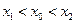 . ………14分
. ………14分
 ,
,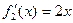 , ………1分
, ………1分依题意,
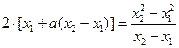 ,得,
,得, . ………3分
. ………3分 (2)
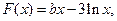
 ,
,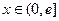 , ………4分
, ………4分①若
 ,
, ,
,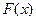 在
在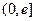 上单调递减,
上单调递减,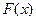 的最小值是
的最小值是 ,由
,由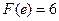 得,
得,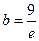 (舍去); ………6分
(舍去); ………6分②若
 ,
,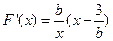 ,令
,令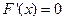 得
得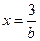 ,
,当
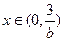 时,
时,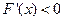 ,
,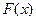 在
在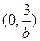 上单调递减;
上单调递减;当
 时,
时,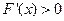 ,
,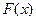 在
在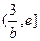 上单调递增;
上单调递增;所以
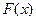 的最小值是
的最小值是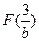 ,由
,由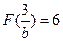 得,
得,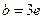 . ………8分
. ………8分(3)
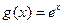 ,结合图象猜测
,结合图象猜测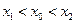 .………9分
.………9分只需证
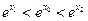 ,∵
,∵ ,
,故只需证
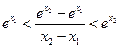 ,
,即证:
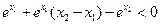 ,且
,且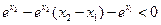 , ………10分
, ………10分设
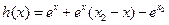 ,
,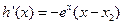 ,当
,当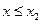 时,
时, ,
,∴
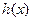 在
在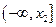 上是增函数,
上是增函数,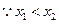 ,∴
,∴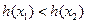 ,而
,而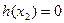
即
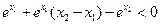 , ………12分
, ………12分设
 ,则
,则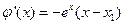 ,当
,当 时,
时,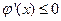 ,
,∴
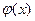 在
在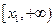 上是减函数,
上是减函数,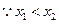 ,∴
,∴ ,而
,而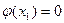
即
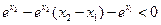 .综上所述,
.综上所述, 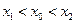 . ………14分
. ………14分略

练习册系列答案
相关题目
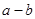 的取值范围为 ( )
的取值范围为 ( ) km.
km. (rad),将
(rad),将
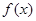 是奇函数,且在
是奇函数,且在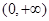 内是增函数,又
内是增函数,又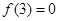 ,则
,则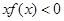 的解集是( )
的解集是( )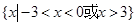
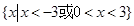
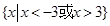
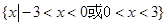
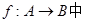 ,
, ,且
,且 ,则与A中的元素
,则与A中的元素 对应的
对应的 中的元素为( )
中的元素为( )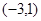

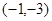
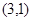
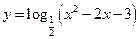 的单调增区间是
的单调增区间是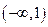 ;
; 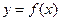 定义域为
定义域为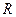 且满足
且满足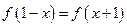 ,则它的图象关于
,则它的图象关于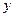 轴对称;
轴对称; 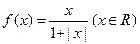 的值域为
的值域为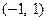 ;
;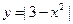 的图象和直线
的图象和直线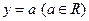 的公共点个数是
的公共点个数是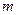 ,则
,则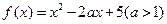 在
在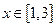 上有零点,则实数
上有零点,则实数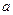 的取值范围是
的取值范围是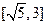 .
.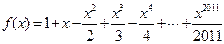 ,
,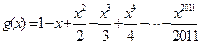 ,设
,设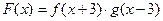 , 且函数
, 且函数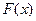 的零点均在区间
的零点均在区间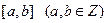 内,则
内,则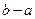 的最小值为________
的最小值为________