题目内容
15.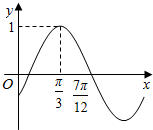 已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cosωx的图象( )
已知函数f(x)=sin(ωx+φ)($ω>0,|φ|<\frac{π}{2}$)的部分图象如图所示,则y=f(x)的图象可由y=cosωx的图象( )| A. | 向右平移$\frac{π}{3}$个长度单位 | B. | 向左平移$\frac{π}{3}$个长度单位 | ||
| C. | 向右平移$\frac{π}{6}$个长度单位 | D. | 向左平移$\frac{π}{6}$个长度单位 |
分析 根据函数的图象求出函数的周期,然后可以求出ω,通过函数经过的最大值点求出φ值,即可得到函数y=Asin(ωx+ϕ)的解析式.根据函数y=Asin(ωx+φ)的图象变换规律即可得解.
解答 解:由函数的图象可知:T=($\frac{7π}{12}$-$\frac{π}{3}$)×4=π,
∴ω=$\frac{2π}{T}$=2.
当x=$\frac{π}{3}$,函数取得最大值1,所以sin(2×$\frac{π}{3}$+φ)=1,可得:$\frac{2π}{3}$+φ=2kπ+$\frac{π}{2}$,k∈Z,
∵|φ|<$\frac{π}{2}$,
∴k=0,φ=-$\frac{π}{6}$
∴f(x)=sin(2x-$\frac{π}{6}$).
∵cos2(x-$\frac{π}{3}$)=cos(2x-$\frac{π}{2}$-$\frac{π}{6}$)=-sin($\frac{π}{6}$-2x)=sin(2x-$\frac{π}{6}$).
∴y=cos2x的图象向右平移$\frac{π}{3}$个长度单位即可得到f(x)=sin(2x-$\frac{π}{6}$)的图象.
故选:A.
点评 本题考查的知识点是由函数y=sin(ωx+ϕ)的部分图象确定其解析式,考查了函数y=Asin(ωx+φ)的图象变换规律,其中φ的求解是解题的关键.

练习册系列答案
相关题目
6.已知f(x)=ax2+bx+c,(a>0),若f(-1)=f(3),则f(-1),f(1),f(4)的大小关系为 ( )
| A. | f(-1)<f(1)<f(4) | B. | f(1)<f(-1)<f(4) | C. | f(-1)<f(4)<f(1) | D. | f(4)<f(-1)<f(1) |
10.已知全集U=R,集合A={x|2<x≤3},集合B={x|2≤x≤4},则(∁UA)∩B等于( )
| A. | {x|3≤x≤4} | B. | {x|3<x≤4} | C. | {x|x=2或3<x≤4} | D. | {x|3<x<4} |
20.函数$f(x)=\sqrt{2x-{x^2}}$的单调递增区间是( )
| A. | (1,+∞) | B. | [0,1] | C. | (-∞,1) | D. | [1,2] |
4.设集合A={x∈Z|x>-1},则( )
| A. | ∅∉A | B. | 2∈A | C. | $\sqrt{2}$∈A | D. | {$\sqrt{2}$}⊆A |