Question

8．过半径为2的圆外一点P作圆的两条切线PA，PB，切点分别为A、B，则$\overrightarrow{PA}$•$\overrightarrow{PB}$的最小值$8\sqrt{2}$-12．

Answer 1

分析 可作出图形，设PA=PB=x，∠APO=α，从而可以得到sin$α=\frac{2}{\sqrt{{x}^{2}+4}}$，cos$∠APB=cos2α=1-\frac{8}{{x}^{2}+4}$，这样便可得出$\overrightarrow{PA}•\overrightarrow{PB}={x}^{2}-\frac{8{x}^{2}}{{x}^{2}+4}$=$（{x}^{2}+4）+\frac{32}{{x}^{2}+4}-12$，这样由基本不等式即可得出$\overrightarrow{PA}•\overrightarrow{PB}$的最小值．

解答 解：如图所示：设PA=PB=x，∠APO=α，OA⊥AP，则：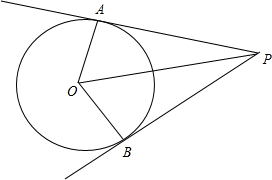

OP=$\sqrt{O{A}^{2}+A{P}^{2}}=\sqrt{{x}^{2}+4}$，sinα=$\frac{2}{\sqrt{{x}^{2}+4}}$；
∴cos∠APB=cos2α=1-2sin²α=$1-\frac{8}{{x}^{2}+4}$；
∴$\overrightarrow{PA}•\overrightarrow{PB}=|\overrightarrow{PA}||\overrightarrow{PB}|cos∠APB$=${x}^{2}（1-\frac{8}{{x}^{2}+4}）={x}^{2}-\frac{8（{x}^{2}+4）-32}{{x}^{2}+4}$=$（{x}^{2}+4）+\frac{32}{{x}^{2}+4}-12$$≥2\sqrt{32}-12=8\sqrt{2}-12$；
∴当${x}^{2}+4=\frac{32}{{x}^{2}+4}$，即x=$\sqrt{4\sqrt{2}-4}$时，$\overrightarrow{PA}•\overrightarrow{PB}$取最小值$8\sqrt{2}-12$．
故答案为：$8\sqrt{2}-12$．

点评 考查圆心和切点的连线垂直于切线，正弦函数的定义，二倍角的余弦公式，向量数量积的计算公式，凑成基本不等式求函数最值的方法，注意判断等号是否成立．