题目内容
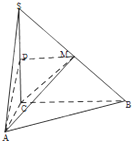 如图:在三棱锥S-ABC中,SC⊥平面ABC,点P,M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角60°
如图:在三棱锥S-ABC中,SC⊥平面ABC,点P,M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角60°(Ⅰ)求证:平面MAP⊥平面SAC;
(Ⅱ)求二面角M-AB-C的平面角的正切值;
(Ⅲ)求AP和CM所成角的余弦值.
分析:(I)根据线面垂直的性质可得SC⊥BC,结合∠ACB=90°及线面垂直的判定定理可得BC⊥平面SAC,由三角形中位线定理可得PM∥BC,结合线面垂直的第二判定定理可得PM⊥平面SAC,最后由面面垂直的判定定理得到平面MAP⊥平面SAC;
(Ⅱ)取BC的中点D,连MD,在平面ABC内作DE⊥AB于E,连ME,可证得∠MED即为二面角M-AB-C的平面角,解三角形MED可得二面角M-AB-C的平面角的正切值;
(Ⅲ)作AF
CD,则AF
PM,可证得∠CMF或其补角即为AP与CM所成的角,解三角形CMF可得AP和CM所成角的余弦值.
(Ⅱ)取BC的中点D,连MD,在平面ABC内作DE⊥AB于E,连ME,可证得∠MED即为二面角M-AB-C的平面角,解三角形MED可得二面角M-AB-C的平面角的正切值;
(Ⅲ)作AF
| ∥ |
. |
| ∥ |
. |
解答:证明:(Ⅰ)∵SC⊥平面ABC,BC?平面ABC,
∴SC⊥BC,
又∵BC⊥AC,SC∩AC=C,SC,AC?平面SAC,
∴BC⊥平面SAC,
∵点P,M分别是SC和SB的中点,
∴PM∥BC,
∴PM⊥平面SAC,
∵PM?平面MAP,
∴平面MAP⊥平面SAC
解:( II)取BC的中点D,连MD,在平面ABC内作DE⊥AB于E,连ME,
由M,D分别为SB,BC的中点,
可得MD∥SC,MD=
SC
由SC⊥平面ABC,可得MD⊥平面ABC,
则∠MED即为二面角M-AB-C的平面角,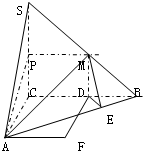
∵直线AM与直线SC所成的角60°,MD∥SC,
∴∠AMD=60°,
∵PM=AC=CD=BD=1,
∴AD=
,MD=
,DE=
,
∴tan∠MED=
=
(Ⅲ)作AF
CD,则AF
PM
即四边形AFMP为平行四边形
则AP∥FM
则∠CMF或其补角即为AP与CM所成的角,
∵CM=
,MF=
,CF=
,
由余弦定理得cos∠CMF=
∴SC⊥BC,
又∵BC⊥AC,SC∩AC=C,SC,AC?平面SAC,
∴BC⊥平面SAC,
∵点P,M分别是SC和SB的中点,
∴PM∥BC,
∴PM⊥平面SAC,
∵PM?平面MAP,
∴平面MAP⊥平面SAC
解:( II)取BC的中点D,连MD,在平面ABC内作DE⊥AB于E,连ME,
由M,D分别为SB,BC的中点,
可得MD∥SC,MD=
| 1 |
| 2 |
由SC⊥平面ABC,可得MD⊥平面ABC,
则∠MED即为二面角M-AB-C的平面角,

∵直线AM与直线SC所成的角60°,MD∥SC,
∴∠AMD=60°,
∵PM=AC=CD=BD=1,
∴AD=
| 2 |
| ||
| 3 |
| ||
| 5 |
∴tan∠MED=
| MD |
| DE |
| ||
| 3 |
(Ⅲ)作AF
| ∥ |
. |
| ∥ |
. |
即四边形AFMP为平行四边形
则AP∥FM
则∠CMF或其补角即为AP与CM所成的角,
∵CM=
| ||
| 3 |
| ||
| 3 |
| 2 |
由余弦定理得cos∠CMF=
| 2 |
| 5 |
点评:本题考查的知识点是平面与平面垂直的判定,异面直线及其所成的角,二面角的平面角及求法,其中构造出空间线面夹角,异面直线夹角的平面角,将空间角问题转化为解三角形问题是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.
如图,在三棱锥S-ABC中,SA⊥平面ABC,平面SAB⊥平面SBC. 如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( )
如图,在三棱锥S-ABC中,G1,G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是( ) 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2 (2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( )
(2013•杭州模拟)如图,在三棱锥S-ABC中,SA=SC=AB=BC,则直线SB与AC所成角的大小是( ) (2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )
(2013•成都一模)如图,在三棱锥S-ABC中,SA丄平面ABC,SA=3,AC=2,AB丄BC,点P是SC的中点,则异面直线SA与PB所成角的正弦值为( )