题目内容
已知函数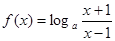
 .
.
(1)判断函数 的奇偶性;
的奇偶性;
(2)判断函数 在
在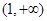 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当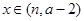 时,函数
时,函数 的值域是
的值域是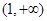 ,求实数
,求实数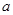 与
与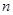 的值;
的值;
(1) 为奇函数。 (2)当
为奇函数。 (2)当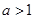 时,
时, 在
在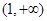 上是减函数.当
上是减函数.当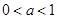 时,
时, 在
在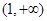 上是增函数. (3)
上是增函数. (3)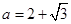 ,
,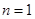 .
.
解析试题分析:(1)由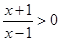 得函数
得函数 的定义域为
的定义域为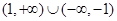 , 2分
, 2分
又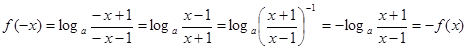
所以 为奇函数。 4分
为奇函数。 4分
(2)由(1)及题设知: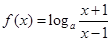 ,设
,设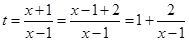 ,
,
∴当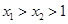 时,
时,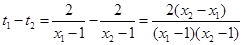 ∴
∴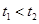 . 6分
. 6分
当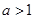 时,
时,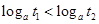 ,即
,即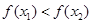 .
.
∴当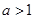 时,
时, 在
在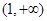 上是减函数.
上是减函数.
同理当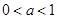 时,
时, 在
在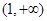 上是增函数. 8分
上是增函数. 8分
(3)①当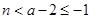 时,有
时,有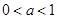 .
.
由(2)可知: 在
在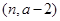 为增函数, 9分
为增函数, 9分
由其值域为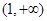 知
知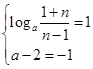 ,无解 10分
,无解 10分
②当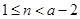 时,有
时,有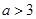 .由(2)知:
.由(2)知: 在
在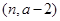 为减函数,
为减函数,
由其值域为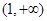 知
知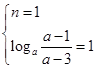 11分
11分
得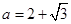 ,
,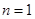 . 12分
. 12分
考点:本题考查了函数的性质
点评:偶函数在关于原点对称的两个区间上的单调性相反,而奇函数在关于原点对称的两个区间上的单调性相同

练习册系列答案
相关题目
 是定义在
是定义在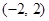 上的奇函数且是减函数,若
上的奇函数且是减函数,若 ,求实数
,求实数 的取值范围。
的取值范围。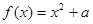 .
.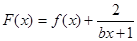 是偶函数,在定义域上
是偶函数,在定义域上 恒成立,求实数
恒成立,求实数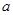 的取值范围;
的取值范围;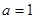 时,令
时,令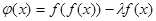 ,问是否存在实数
,问是否存在实数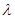 ,使
,使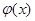 在
在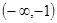 上是减函数,在
上是减函数,在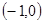 上是增函数?如果存在,求出
上是增函数?如果存在,求出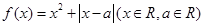 .
.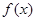 的奇偶性;
的奇偶性;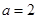 时,求
时,求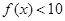 对
对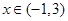 恒成立,求实数
恒成立,求实数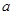 的取值范围.
的取值范围.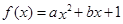 在
在 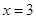 处的切线方程为
处的切线方程为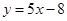 .
.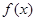 的解析式;
的解析式;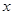 的方程
的方程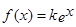 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数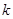 的值 ;
的值 ;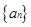 满足
满足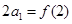 ,
,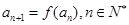 ,求
,求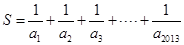 的整数部分.
的整数部分. 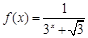 ,(1)分别求
,(1)分别求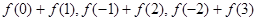 ;(2)然后归纳猜想一般性结论,并给出证明.
;(2)然后归纳猜想一般性结论,并给出证明. 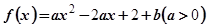 在区间
在区间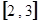 上的值域为
上的值域为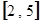
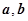 的值;
的值;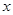 的函数
的函数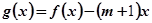 在区间
在区间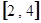 上为单调函数,求实数
上为单调函数,求实数 的取值范围.
的取值范围. 
 .
.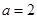 时,求
时,求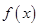 的极值;
的极值;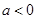 时,讨论
时,讨论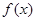 的单调性;
的单调性;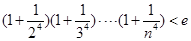 (
(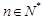 ,
,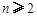 ,其中无理数
,其中无理数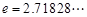 )
) .
.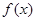 为定义域上的单调函数,求实数m的取值范围;
为定义域上的单调函数,求实数m的取值范围;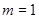 ,
,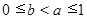 时,证明:
时,证明: .
.