题目内容
(不等式4-5)已知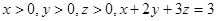 ,那么
,那么
 的最小值为 ;
的最小值为 ;
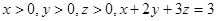 ,那么
,那么 的最小值为 ;
的最小值为 ;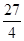 .
. 试题分析:根据柯西不等式,[
 ](1+1+1)≥[(x+2y+3z)+
](1+1+1)≥[(x+2y+3z)+ 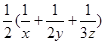 ]
] =[3+
=[3+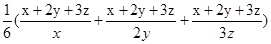 ]
]
=[3+
 ]
] ≥(3+
≥(3+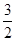 )²=
)²=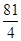
所以
 ≥
≥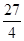 ,
, 的最小值为
的最小值为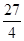 。
。等号成立条件,按柯西不等式“=”成立的条件可以确定 。
点评:中档题,根据已知条件,通过构造应用“柯西不等式”的条件,应用柯西不等式求得最值。

练习册系列答案
相关题目
题目内容
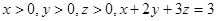 ,那么
,那么 的最小值为 ;
的最小值为 ;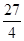 .
.  ](1+1+1)≥[(x+2y+3z)+
](1+1+1)≥[(x+2y+3z)+ 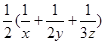 ]
] =[3+
=[3+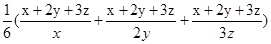 ]
]
 ]
] ≥(3+
≥(3+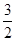 )²=
)²=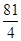
 ≥
≥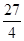 ,
, 的最小值为
的最小值为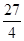 。
。