Question

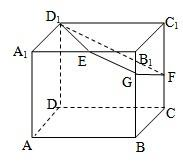如图，已知正方体ABCD-A₁B₁C₁D₁的棱长为2，E、F分别是A₁B₁、CC₁的中点，过D₁、E、F作平面D₁EGF交BB₁于G．
（Ⅰ）求证：EG∥D₁F；
（Ⅱ）求二面角C₁-D₁E-F的余弦值；
（Ⅲ）求正方体被平面D₁EGF所截得的几何体ABGEA₁-DCFD₁的体积．

Answer 1

分析：（I）根据正方体的几何特征及面面平行的性质定理，易证得EG∥D₁F；
（Ⅱ）以D为原点分别以DA、DC、DD₁为x、y、z轴，建立空间直角坐标系，分别求出平面D₁EGF的法向量和平面ABCD的法向量，代入向量夹角公式，即可得到答案；
（III）几何体ABGEA₁-DCFD₁由正方体ABCD-A₁B₁C₁D₁减去一个棱台D₁FC₁-EGB₁得到，分别求出正方体ABCD-A₁B₁C₁D₁的体积和棱台D₁FC₁-EGB₁的体积，即可得到答案．

解答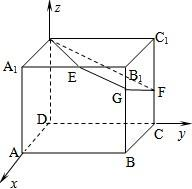：证明：（Ⅰ）在正方体ABCD-A₁B₁C₁D₁中，∵平面ABB₁A₁∥平面DCC₁D₁
平面D₁EGF∩平面ABB₁A₁=EG，平面D₁EGF∩平面DCC₁D₁=D₁F，
∴EG∥D₁F．（3分）
解：（Ⅱ）如图，以D为原点分别以DA、DC、DD₁为
x、y、z轴，建立空间直角坐标系，则有
D₁（0，0，2），E（2，1，2），F（0，2，1），
∴

D1E

=（2，1，0），

D1F

=（0，2，-1）
设平面D₁EGF的法向量为

n

=（x，y，z）
则由

n

•

D1E

=0，和

n

•

D1F

=0，得

2x+y=0 2y-z=0

，
取x=1，得y=-2，z=-4，∴

n

=（1，-2，-4）（6分）
又平面ABCD的法向量为

DD1

（0，0，2）
以二面角C₁-D₁E-F的平面角为θ，
则cosθ=|

DD1 • n

|DD1 |•| n |

|=

4 21

21

故截面D₁EGF与底面ABCD所成二面角的余弦值为

4 21

21

．（9分）
解：（Ⅲ）设所求几何体ABGEA₁-DCFD₁的体积为V，
∵△EGB₁∽△D₁FC₁，D₁C₁=2，C₁F=1，
∴EB₁=

1

2

D₁C₁=1，B₁G=

1

2

C₁F=

1

2

，
∴S△EB1G=

1

2

EB₁•B₁G=

1

2

•1•

1

2

=

1

4

，
S△D1FC1=

1

2

D₁C₁•C₁F=

1

2

•2•1=1（11分）
故V_{棱台D1FC1-EGB1}=

7

6

∴V=V_正方体-V_{棱台D1FC1-EGB1}=2³-

7

6

=

41

6

．（14分）

点评：本题考查的知识点是用空间向量求平面间的夹角，组合体的体积，线线平行的判定，其中（1）的关键是熟练掌握线线平行、线面平行、面面平行之间的相互转化，（2）的关系是求出平面D₁EGF的法向量和平面ABCD的法向量，（3）的关键是分析出几何体ABGEA₁-DCFD₁由正方体ABCD-A₁B₁C₁D₁减去一个棱台D₁FC₁-EGB₁得到．