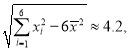题目内容
【题目】在平面直角坐标系中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点(异于原点
两点(异于原点![]() ),定点
),定点![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)将曲线C1化成直角坐标方程,再化成极坐标方程;(2)先求出定点M到射线的距离
为三角形的高,再由极坐标方程求出弦长|AB|为三角形的底,根据面积公式求解即可.
(1)解:曲线C1直角坐标方程为:x2+y2﹣4y=0,
由ρ2=x2+y2,ρsinθ=y得:
曲线C1极坐标方程为ρ=4sinθ,
(2)法一:M到射线θ=![]() 的距离为d=2sin
的距离为d=2sin![]() =
=![]() ,
,
|AB|=ρB﹣ρA=4(sin![]() ﹣cos
﹣cos![]() )=2(
)=2(![]() ﹣1)
﹣1)
则S△MAB=![]() |AB|×d=3﹣
|AB|×d=3﹣![]() .
.
法二:
解:将θ=![]() (ρ≥0)化为普通方程为y=
(ρ≥0)化为普通方程为y=![]() x(x≥0),
x(x≥0),
∵曲线C2的极坐标方程为ρ=4cosθ,即ρ2=4ρcosθ,
由ρ2=x2+y2,ρcosθ=x得:
曲线C2的直角坐标方程为x2+y2﹣4x=0,
由![]() 得
得![]() ∴A(
∴A(![]() ,3)
,3)
![]() 得
得![]() ∴B(1,
∴B(1,![]() ),
),
![]() ,
,
点M到直线![]() ,
,
∴![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】第二届中国国际进口博览会于2019年11月5日至10日在上海国家会展中心举行.它是中国政府坚定支持贸易自由化和经济全球化,主动向世界开放市场的重要举措,有利于促进世界各国加强经贸交流合作,促进全球贸易和世界经济增长,推动开放世界经济发展.某机构为了解人们对“进博会”的关注度是否与性别有关,随机抽取了100名不同性别的人员(男、女各50名)进行问卷调查,并得到如下![]() 列联表:
列联表:
男性 | 女性 | 合计 | |
关注度极高 | 35 | 14 | 49 |
关注度一般 | 15 | 36 | 51 |
合计 | 50 | 50 | 100 |
(1)根据列联表,能否有99.9%的把握认为对“进博会”的关注度与性别有关;
(2)若从关注度极高的被调查者中按男女分层抽样的方法抽取7人了解他们从事的职业情况,再从7人中任意选取2人谈谈关注“进博会”的原因,求这2人中至少有一名女性的概率.
附:![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |