题目内容
(本小题共14分)
已知椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,短轴两个端点为
,短轴两个端点为![]() 、
、![]() ,且四
,且四
边形![]() 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆的方程;
(2)若![]() 、
、![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点![]() 满足
满足![]() ,连结
,连结![]() ,交椭圆于点
,交椭圆于点![]() .证明:
.证明:![]() 为定值;
为定值;
(3)在(2)的条件下,试问![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点Q,使得以
的定点Q,使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() 的交点,若存在,求出点Q的坐标;若不存在,说明理由.
的交点,若存在,求出点Q的坐标;若不存在,说明理由.
(本小题共14分)
解:(Ⅰ)如图,由题意得,![]() ,
,![]()
![]() ,
,![]() .
.

![]() 所求的椭圆方程为
所求的椭圆方程为![]() . …………………………………3分
. …………………………………3分
(Ⅱ)由(Ⅰ)知,![]() (
(![]() ,0),
,0),![]() (2,0). ………………………………………4分
(2,0). ………………………………………4分
由题意可设![]() :
:![]() ,
,![]() (
(![]() ,
,![]() ).
).
![]()
![]() ,
,![]()
![]() (2,
(2,![]() ). ……………5分
). ……………5分
由  整理得:
整理得:![]() .
.
![]()
![]() ,
, ![]()
![]() . ………………………………………7分
. ………………………………………7分
![]()
![]() ,
,![]() . ………………………………………8分
. ………………………………………8分
![]()
![]() . ………………………………………9分
. ………………………………………9分
即![]() 为定值.
为定值.
(Ⅲ)设![]() ,则
,则![]() .
.
若以![]() 为直径的圆恒过
为直径的圆恒过![]() ,
,![]() 的交点,则
的交点,则![]() ,
,![]()
![]() 恒成立.……10分
恒成立.……10分
由(Ⅱ)可知![]() ,
,![]() . ………………………………12分
. ………………………………12分
![]()
![]() .即
.即![]() 恒成立.
恒成立.![]()
![]() .
.
![]() 存在
存在![]() 使得以
使得以![]() 为直径的圆恒过直线
为直径的圆恒过直线![]() ,
,![]() 的交点. ……………………………14分
的交点. ……………………………14分

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是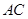 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.