Question

【题目】已知椭圆.点E为椭圆在第一象限内一点，点F在椭圆上且与点E关于原点对称，直线与椭圆交于A，B两点，则点E，F到直线x+y-1=0的距离之和的最大值是________；此时四边形AEBF的面积是________.

Answer 1

【答案】

【解析】

根据题意，设出两点坐标，利用点到直线的距离公式，求得距离之和的表达式，结合点在椭圆上坐标满足椭圆方程，利用柯西不等式即可求得距离之和的最大值；联立椭圆方程和，求得两点坐标，即可求得，则四边形的面积可得.

根据题意，作图如下：

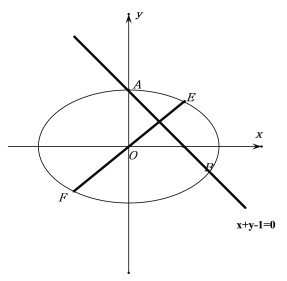
不妨设，则，

故到直线的距离之和

因为点是椭圆上位于第一象限的点，根据直线划分平面，以及点位于直线的右上侧，

故可得：，且，

则.

又因为点在椭圆上，故，

由柯西不等式可得：，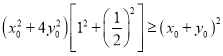

即，解得，当且仅当时取得等号.

故；

联立椭圆方程与直线方程，

可得，解得，

故可得.

故四边形的面积.

故答案为：；.