题目内容
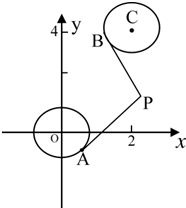 已知圆O:x2+y2=1,圆C:(x-2)2+(y-4)2=1.在两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,满足|PA|=|PB|.
已知圆O:x2+y2=1,圆C:(x-2)2+(y-4)2=1.在两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,满足|PA|=|PB|.(1)求实数a,b间的关系式.
(2)求切线长|PA|的最小值.
(3)是否存在以P为圆心的圆,使它与圆O相内切并且与圆C相外切,若存在求出圆P的方程,若不存在,请说明理由.
分析:(1)连接PO,PC,利用|PA|=|PB|.结合半径,推出实数a,b间的关系式.
(2)利用(1)的结论,通过勾股定理求出切线长|PA|的表达式,利用配方法求出最小值.
(3)设存在以P为圆心的圆,设出半径,利用|PC|=|PO|+2,结合勾股定理推出
=4-(a+2b)=-1<0,说明故满足条件的圆不存在.
(2)利用(1)的结论,通过勾股定理求出切线长|PA|的表达式,利用配方法求出最小值.
(3)设存在以P为圆心的圆,设出半径,利用|PC|=|PO|+2,结合勾股定理推出
| a2+b2 |
解答:解:(1)连接PO,PC,∵|PA|=|PB|,|0A|=|CB|=1,
∴|PO|2=|PC|2从而a2+b2=(a-2)2+(b-4)2,a+2b-5=0.
(2)由(1)得a=-2b+5
∴|PA|=
=
=
=
当b=2时,|PA|min=2.
(3)若存在,设半径为R,则有|PO|=R-1,|PC|=R+1,于是|PC|=|PO|+2,
即
=
+2
整理得
=4-(a+2b)=-1<0
故满足条件的圆不存在.
∴|PO|2=|PC|2从而a2+b2=(a-2)2+(b-4)2,a+2b-5=0.
(2)由(1)得a=-2b+5
∴|PA|=
| |PO|2-|OA|2 |
| a2+b2-1 |
| 5b2-20b+24 |
| 5(b-2)2+4 |
当b=2时,|PA|min=2.
(3)若存在,设半径为R,则有|PO|=R-1,|PC|=R+1,于是|PC|=|PO|+2,
即
| (a-2)2+(b-4)2 |
| a2+b2 |
整理得
| a2+b2 |
故满足条件的圆不存在.
点评:本题是中档题,考查直线与圆的位置关系,勾股定理的应用,存在性问题的解法,考查计算能力,推理能力.

练习册系列答案
相关题目
 已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为
已知圆O:x2+y2=2交x轴于A,B两点,曲线C是以AB为长轴,离心率为 已知圆o:x2+y2=b2与椭圆
已知圆o:x2+y2=b2与椭圆