题目内容
已知抛物线方程y2=4x,直线l的方程为x-y+5=0,在抛物线上有一动点P到y轴的距离为d1,到直线l的距离为d2,则d1+d2的最小值为 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据抛物线的定义可知:d1+d2的最小值为焦点到直线l的距离减去1,运用点到直线的距离公式求解即可.
解答:
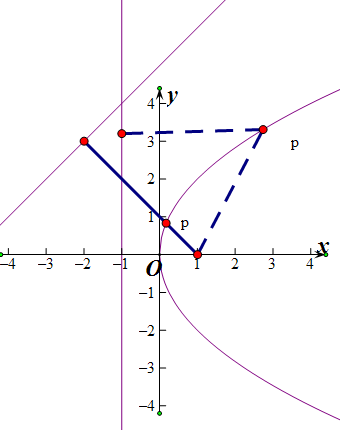 解:∵抛物线方程y2=4x,直线l的方程为x-y+5=0,
解:∵抛物线方程y2=4x,直线l的方程为x-y+5=0,
∴F(1,0)准线为x=-1,
∵在抛物线上有一动点P到y轴的距离为d1,到直线l的距离为d2,
∴根据抛物线的定义可知:d1+d2的最小值为焦点到直线l的距离减去1,
∴最小值为
-1=3
-1,
故答案为:3
-1
 解:∵抛物线方程y2=4x,直线l的方程为x-y+5=0,
解:∵抛物线方程y2=4x,直线l的方程为x-y+5=0,∴F(1,0)准线为x=-1,
∵在抛物线上有一动点P到y轴的距离为d1,到直线l的距离为d2,
∴根据抛物线的定义可知:d1+d2的最小值为焦点到直线l的距离减去1,
∴最小值为
| |1-0+5| | ||
|
| 2 |
故答案为:3
| 2 |
点评:本题考查了抛物线的定义,运用图象求解最小值的问题,属于中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
已知函数f(x)=2sin(-2x+
)+1,若x∈(-
,
),则函数f(x)的值域为( )
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
A、(1-
| ||||
B、(1-
| ||||
C、[-1,1+
| ||||
| D、[-1,3] |
为了准备晚饭,小张找出了5种不同的新鲜蔬菜和4种冷冻蔬菜.如果晚饭时小张只吃1种蔬菜,不同的选择种数是( )
| A、5 | B、4 | C、9 | D、20 |
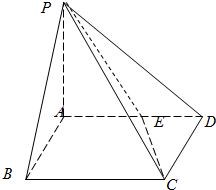 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E为棱AD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E为棱AD的中点.