题目内容
某高校在2013年考试成绩中100名学生的笔试成绩的频率分布直方图如图所示,
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
① 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙不同时进入第二轮面试的概率;
② 若第三组被抽中的学生实力相当,在第二轮面试中获得优秀的概率均为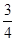 ,设第三组中被抽中的学生有
,设第三组中被抽中的学生有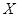 名获得优秀,求
名获得优秀,求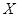 的分布列和数学期望。
的分布列和数学期望。
(1)0.3,0.2,0.1
(2)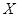 的分布列如下:
的分布列如下: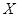
0 1 2 3 
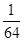
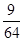
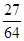
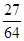
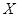 的数学期望
的数学期望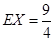
解析试题分析:解:(1)第三组的频率为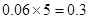 ;第四组的频率为
;第四组的频率为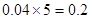 ;
;
第五组的频率为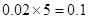 3分
3分
(2)①设学生甲和学生乙同时进入第二轮面试为事件M:则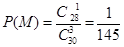
所以学生甲和学生乙不同时进入第二轮面试的概率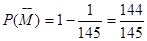 7分
7分
②由已知得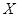 ~
~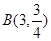 ,且
,且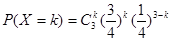 ,
,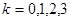 ,
,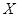 的分布列如下:
的分布列如下: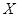
0 1 2 3 
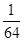
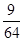
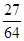
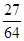
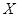 的数学期望
的数学期望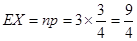 13分
13分
考点:概率分布列
点评:主要是考查了古典概型概率公式的运用,以及分布列的求解和期望公式,属于基础题。

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
为了保养汽车,维护汽车性能,汽车保养一般都在购车的4S店进行,某地大众汽车4S店售后服务部设有一个服务窗口专门接待保养预约。假设车主预约保养登记所需的时间互相独立,且都是整数分钟,对以往车主预约登记所需的时间统计结果如下:
| 登记所需时间(分) | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
(l)估计第三个车主恰好等待4分钟开始登记的概率:
(2)X表示至第2分钟末已登记完的车主人数,求X的分布列及数学期望.
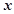 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。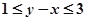 的概率;
的概率;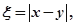 求随机变量
求随机变量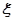 的分布列和数学期望。
的分布列和数学期望。 ,乙队每人答对的概率都是
,乙队每人答对的概率都是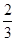 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用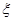 表示甲队总得分.
表示甲队总得分.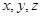 分别表示甲,乙,丙3个盒中的球数.
分别表示甲,乙,丙3个盒中的球数.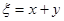 ,求随机变量
,求随机变量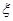 的概率分布列和数学期望.
的概率分布列和数学期望.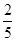 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是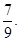
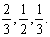 用
用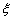 表示被招聘的人数。
表示被招聘的人数。