题目内容
已知定义在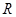 上的奇函数
上的奇函数 在
在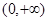 上单调递增,且
上单调递增,且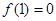 ,则不等式
,则不等式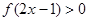 的解集为 .
的解集为 .
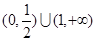
解析试题分析:由题意得: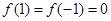 ,不等式
,不等式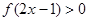 的解集为
的解集为 或
或 ,解得
,解得
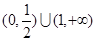 .
.
考点:函数的性质、不等式的解法.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
题目内容
已知定义在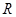 上的奇函数
上的奇函数 在
在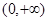 上单调递增,且
上单调递增,且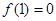 ,则不等式
,则不等式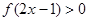 的解集为 .
的解集为 .
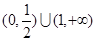
解析试题分析:由题意得: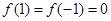 ,不等式
,不等式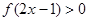 的解集为
的解集为 或
或 ,解得
,解得
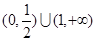 .
.
考点:函数的性质、不等式的解法.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案