题目内容
11.已知函数f(x)是定义在R上的奇函数,且是以4π为最小正周期的周期函数.(1)若f(x)=cos(ωx+φ)(ω>0,φ∈[0,$\frac{π}{2}$]),求ω和φ的值;
(2)若α是第一象限的角,当sinα=$\frac{1}{3}$时,求f(16$\sqrt{2}$π•tanα)的值.
分析 (1)根据余弦型函数的图象和性质,结合函数的奇偶性和周期,可得ω和φ的值;
(2)若α是第一象限的角,当sinα=$\frac{1}{3}$时,f(16$\sqrt{2}$π•tanα)=f(8π),代入计算可得答案.
解答 解:(1)∵函数f(x)是定义在R上的奇函数,且是以4π为最小正周期的周期函数
若f(x)=cos(ωx+φ)(ω>0,φ∈[0,$\frac{π}{2}$]),
则ω=$\frac{2π}{4π}$=$\frac{1}{2}$,
cosφ=0,φ=$\frac{π}{2}$
(2)若α是第一象限的角,当sinα=$\frac{1}{3}$时,
cosα=$\frac{2\sqrt{2}}{3}$,tanα=$\frac{1}{2\sqrt{2}}$,
则f(16$\sqrt{2}$π•tanα)=f(8π)=cos($\frac{1}{2}$×8π+$\frac{π}{2}$)=cos$\frac{π}{2}$=0
点评 本题考查的知识点是余弦型函数的图象和性质,函数的奇偶性和周期,难度中档.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
19.设y=f(2-x)可导,则y′等于( )
| A. | f′(2-x)1n2 | B. | 2-x•f′(2-x)1n2 | C. | -2-x•f′(2-x)1n2 | D. | -2-x•f′(2-x)1og22 |
3.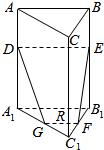 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D、E分别在AA1、BB1上,AD=BE=1,F、G分别是B1C1、A1C1的中点,则直线GF与直线DE的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D、E分别在AA1、BB1上,AD=BE=1,F、G分别是B1C1、A1C1的中点,则直线GF与直线DE的距离为( )
 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D、E分别在AA1、BB1上,AD=BE=1,F、G分别是B1C1、A1C1的中点,则直线GF与直线DE的距离为( )
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D、E分别在AA1、BB1上,AD=BE=1,F、G分别是B1C1、A1C1的中点,则直线GF与直线DE的距离为( )| A. | $\sqrt{3}$ | B. | $\frac{3\sqrt{6}}{4}$ | C. | $\frac{2\sqrt{5}}{3}$ | D. | $\frac{\sqrt{19}}{2}$ |