题目内容
数列{an}的前n项和为Sn,若Sn=2an-1(n∈N*),则Tn=
+
+…+
的结果可化为( )
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
A、1-
| ||||
B、1-
| ||||
C、
| ||||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:由已知条件推导出an=2n-1,从而
=
,由此能求出Tn=
+
+…+
的表达式.
| 1 |
| anan+1 |
| 1 |
| 22n-1 |
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
解答:
解:∵Sn=2an-1(n∈N*),
∴n=1时,a1=S1=2a1-1 ,解得a1=1.
n≥2时,an=Sn-Sn-1=2an-2an-1,
∴an=2an-1,
∴an=2n-1,
=
,
∴Tn=
+
+…+
=
+
+
+…+
=
=
(1-
).
故选:C.
∴n=1时,a1=S1=2a1-1 ,解得a1=1.
n≥2时,an=Sn-Sn-1=2an-2an-1,
∴an=2an-1,
∴an=2n-1,
| 1 |
| anan+1 |
| 1 |
| 22n-1 |
∴Tn=
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
=
| 1 |
| 2 |
| 1 |
| 23 |
| 1 |
| 25 |
| 1 |
| 22n-1 |
=
| ||||
1-
|
=
| 2 |
| 3 |
| 1 |
| 4n |
故选:C.
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
若直线(1+a)x+y-1=0与圆x2+y2+4x=0相切,则a的值为( )
| A、1或-1 | ||||
B、
| ||||
| C、1 | ||||
D、-
|
下列函数中,增长速度最快的是( )
| A、y=20x |
| B、y=x20 |
| C、y=log20x |
| D、y=20x |
| cos20°sin20° |
| cos225°-sin225° |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
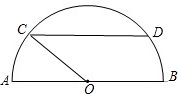 如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧
如图是一个半圆形湖面景点的示意图,已知AB为直径,且AB=2km,O为圆心,C为圆周上靠近A的一点,D为圆周上靠近B的一点,且CD∥AB,现在准备从A经过C到D建造一条观光路线,其中A到C是圆弧